Math 75A Practice Midterm I Solutions
DISCLAIMER. This collection of practice problems is
not guaranteed to be identical, in
length or content, to the actual exam. You may expect to see problems on the
test that are not
exactly like problems you have seen before.
Multiple Choice . Circle the letter of the best
answer.
1. A description for the function 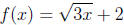 is
is
(a) Take 3 times a number and then add 2
(b) Take 3 times a number, add 2, and then take the square root of the result
| (c) | Take 3 times a number, take the square root of the result , then add 2 |
(d) Take 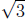 times a
number and then add 2
times a
number and then add 2
3x is under the square root, so we are taking the input and multiplying it by 3,
then taking
the square root of the result. Finally, we add 2.
2. The range of the function g(x) = −x2 + 6x + 5 is
(a) R (all real numbers )
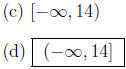
g(x) is a parabola opening down, so the range (outputs)
must be from −∞ to the ycoordinate
of the vertex. The vertex is at (3, 14) (for a reminder of how to find the
vertex
of a parabola, see p. 67-68 of Ebersole). Since 14 is in the range, and −∞ is
not (−∞ is
not a real number!), the range is 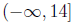 .
.
3. The graph of the function
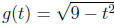 is
is
(a) A circle of radius 9 centered at the origin
(b) A circle of radius 3 centered at the origin
(c) The upper half of a circle of radius 9 centered at the origin
| (d) | The upper half of a circle of radius 3 centered at the origin |
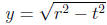 always represents the upper half of a circle of radius r centered at the
origin,
always represents the upper half of a circle of radius r centered at the
origin,
since if we square both sides we get y2 = r2 − t2, or t2 + y2 = r2, which is the
equation of
a circle of radius r. We get only the upper half because
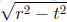 cannot be negative for
cannot be negative for
any input t.
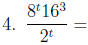

We can express everything in the fraction with base 2, as
follows: 8 = 23 and 16 = 24, so
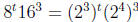 , which simplifies to
, which simplifies to
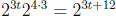 . Finally, we subtract
the exponents
. Finally, we subtract
the exponents
of the top and bottom to get
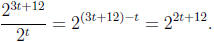
5. The inverse of the function f(x) = 5x3 is

To compute the inverse of a one-to-one function, switch y
and x, then solve for the new
y. We have
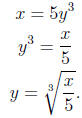
So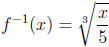 . To check, you can verify that
. To check, you can verify that 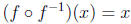 :
:
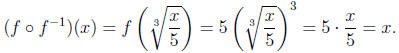
6. If f(x) is a one-to-one function and f(−3) = 2 and f(2) = −5, then f -1(2) =

The inverse of a function has the x’s and y’s switched
from the original function. In other
words, if f(a) = b, then f -11(b) = a. Here we are told that f(−3) = 2, so we know
f -1(2) = −3.
Fill-In. If f(x) = 3x − 5 and g(x) = ex, then
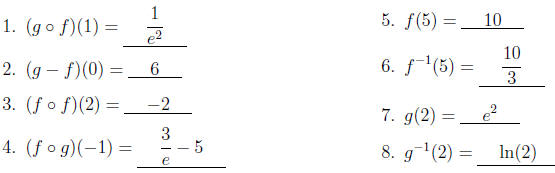
#5 and #7 are easy, so we’ll start with those. We have
f(5) = 3(5) − 5 = 15 − 5 = 10 and
g(2) = e2.
The rest of these problems can be done in two ways . You can either just plug in
the specific
inputs into each function, or you can compute the formulas for
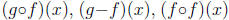 ,
,
etc. and then plug in the values to each new formula.
| Prev | Next |