Math Homework #6 Solutions

p 315, #4 Let 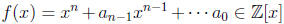and suppose that x−r divides f (x) for
some r ∈Q. Then we must have f(r) = 0. We will use this fact to prove that in fact r ∈Z.
If r = 0 then there is nothing to prove. So assume r ≠ 0 and write r = a/b with a, b ∈Z,
b ≠ 0 and (a, b) = 1. Then

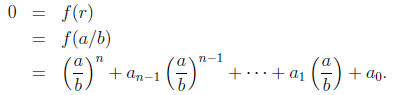
Multiplying both sides by bⁿ then yields

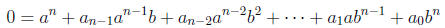
which is equivalent to

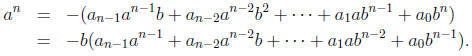
Since 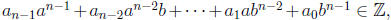this implies that b divides a ⁿ. Since
(a, b) = 1, this can only occur if b = ±1. But then r = a/b = ±a ∈ Z, as claimed.

p 315, #6 If p is prime and f(x) ∈ Z_p[x] is irreducible then 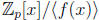is a field by
Corollary 1 to Theorem 17.5, since Z_p is a field. Moreover, we proved in class that since
deg f(x) = n the each element of 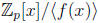can be expressed uniquely as
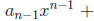
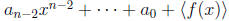for some a_i ∈ F. Since there are p choices for each coefficient
a_i and n coefficients, there are exactly pⁿ such cosets. That is, 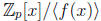is a field with
pⁿ elements.

p 316, #8 Let f(x) = x³ + 2x + 1 ∈ Z₃[x]. It is easy to show that f(x) has no roots in Z₃
and as deg f(x) = 3, this implies f(x) is irreducible in Z₃[x]. So according to Exercise #6,
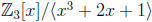is a field with 3³ = 27 elements.

p 316, #10

a. x⁵ + 9x⁴ + 12x² + 6 is irreducible according Eisenstein’s criterion with p = 3.

b. Consider x⁴ + x + 1 mod 2. It is easy to see that this polynomial has no roots in Z₂,
and so to prove irreducibility in Z₂ it suffices to show it has no quadratic factors. The
only quadratic polynomial in Z₂[x] that does not have a root in Z₂ is x² + x + 1 which
does not divide x⁴ + x + 1 in Z₂[x], as is also easily checked. It follows that x⁴ + x + 1
is irreducible in Z₂[x] and so by the mod p test with p = 2 we conclude that x⁴ + x + 1
is irreducible in Q[x].

c. x⁴ + 3x² + 3 is irreducible according to Eisenstein’s criterion with p = 3.

d. Consider x⁵ +5x² +1 mod 2, which is x⁵ +x² +1. It is easy to see that this polynomial
has no roots in Z ₂, and so to prove irreducibility in Z₂ it again suffices to show it has
no quadratic factors. The only quadratic polynomial in Z ₂[x] that does not have a root
in Z₂ is x² + x + 1 which does not divide x⁵ + x² + 1 in Z₂[x], as is also easily checked.
It follows that x⁵ + x² + 1 is irreducible in Z₂[x] and so by the mod p test with p = 2
we conclude that x⁵ + 5x² + 1 is irreducible in Q[x].

e. Let f(x) = (5/2)x⁵ + (9/2)x⁴ + 15x³ + (3/7)x² + 6x + 3/14 and g(x) = 35x⁵ + 63x⁴ +
210x³ +6x² +84x+3 = 14f(x). Since 14 is a unit in Q[x], f(x) is irreducible in Q[x] if
and only if g(x) is, and the latter statement is true by Eisenstein’s criterion with p = 3.

p 316, #12 Since it has degree 2, to show that x² +x+4 is irreducible in Z₁1[x] it suffices
to show it has no roots in Z ₁₁, as Z₁₁ is a field. This is straightforward and is left to the
reader.

p 316, #16
a. Since Z_p is a field, a polynomial of the form x² + ax + b ∈ Z_p[x] is reducible if and
only if there exist c, d ∈ Z₁₁ so that x² + ax + b = (x + c)(x + d). There are 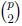such
polynomials for which c ≠ d and p for which c = d. Therefore, there are exactly

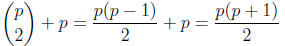
reducible monic quadratic polynomials in Z_p[x]. Since there are p² polynomials of the
form x² + ax + b and each one is either reducible or irreducible, we conclude there are

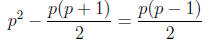
irreducible monic degree 2 polynomials in Z_p[x].

b. If f(x) ∈ Z_p[x] is irreducible of degree 2, then f(x) = ag(x) for some a ∈ F, a ≠ 0
and g(x) ∈ F[x] irreducible, monic and of degree 2. There are p − 1 choices for a and,
by part (a), p(p − 1)/2 choices for g(x). Therefore there are p(p − 1)²/2 irreducible
quadratic polynomials in Z_p[x].

p 316, #24 Substituting all of the elements of Z₇ into 3x² + x + 4 we find that it has two
roots: 4 and 5. The quadratic formula “predicts” the roots

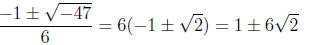
since 6^-1 = 6 in Z₇ and −47 = 2 in Z₇. Since 3² = 9 = 2 in Z₇, we can take 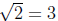and so
the two predicted roots are

1 ± 6 · 3 = 4, 5

which agree with those found by substitution.
If we substitute all of the elements of Z₅ into 2x² +x+3 we find no roots. The quadratic
formula predicts the roots are

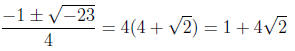
since 4^-1= 4 and −23 = 2 in Z₅. p However, there is no element in Z₅ whose square is 2, so
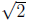is not an element of Z₅. Consequently the roots predicted by the quadratic formula do
not belong to Z₅, which is in agreement with the fact that there are no roots in Z₅.

It turns out that the quadratic formula alwaysgives the roots of ax² + bx + c ∈ F[x] for
any field F, as long as we agree that if b² − 4ac is not a square in F then we interpret the
formula as yielding no roots. This is easily proven using the usual proof of the quadratic
formula (i.e. completing the square ).

p 317, #28 Let f(x) ∈ Q[x] be nonzero. Choose an n ∈ Z⁺ so that g(x) = nf(x) ∈ Z[x].
Since n ≠ 0 it is a unit in Q[x]. So f(x) is irreducible in Q[x] if and only if g(x) is, and the
latter’s irreducibility can be tested using the mod p test.

p 317, #30 Let 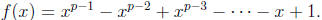If p = 2 then the polynomial in
question is x − 1 which is obviously irreducible in Q[x]. If p > 2 then it is odd and so

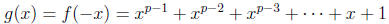
is the pth cyclotomic polynomial, which is irreducible according to the Corollary of Theorem
17.4. It follows that f(x) is irreducible, for if f(x) factored so too would g(x).

p 317, #32 Let f(x), g(x) ∈ Z[x] and suppose that 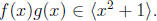Then there is an
h(x) ∈ Z[x] so that f(x)g(x) = (x² + 1)h(x). Since x² + 1 is primitive and irreducible in
Q[x], it is also irreducible in Z[x]. We apply Theorem 17.6 to write

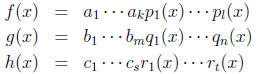
where the a_i, b_i and c_i are primes in Z and the p_i(x), q_i(x) and r_i(x) are irreducible polynomials
of positive degree in Z[x]. Substituting these expressions into f (x)g(x) = (x² +1)h(x)
and rearranging we obtain

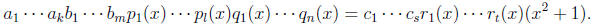
Theorem 17.6 and the irreducibility of x² + 1 now imply that x² + 1 = ±p_i(x) for some i or
x² + 1 = ±q_i(x) for some i. In the first case x² + 1 divides f(x) and in the second x² + 1
divides g(x). That is, either 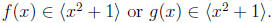Therefore 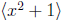is prime
in Z[x].

Let p ∈ Z⁺ be any prime. We will show that 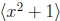is properly contained in
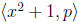
which is not equal to Z[x]. This will prove that 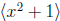is not maximal. Since every nonzero
element of 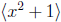has degree at least 2, 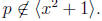This proves that 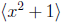is properly
contained in 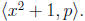Now suppose, for the sake of contradiction, that
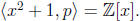
Then there exist f(x), g(x) ∈ Z[x] so that f(x)(x² + 1) + g(x)p = 1. If we consider this
equation mod p we obtain 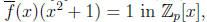which is impossible since
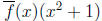
in Z_p[x] is either 0 or has degree at least 2. This contradiction establishes that 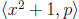is
not equal to Z[x], which completes the proof that 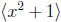is not maximal in Z[x].