Get it on Google Play Get it on Apple Store

Math Practice Test #2 Solutions

I. Be able to graph a polynomial function, or obtain the equa-
tion of a polynomial from its graph

1. Let p(x) = x2(x - 3)(x + 4).
a. (2 pts) What is the domain of p(x)?
b. (3 pts) Find the zero(s) of p(x). Write them as ordered pairs (x, y).
c. (3 pts) Determine whether the graph of p(x) crosses or touches at each
x-intercept.
d. (2 pts) Find the y-intercept. Write it as an ordered pair (x, y).
e. (1 pt) What is the degree of p(x)?
f. (1 pt) What is the maximum number of turning points in the graph of
p(x)?
g. (2 pts) Describe the end behavior of p(x) graphically or analytically.
h. (6 pts) Use the above information and additional test points (as needed)
to sketch the graph of p(x). These points should be labeled on your graph.
Neatness counts!

This problem was taken directly from our quiz. See quiz solutions
for details.

2. Repeat steps a-h in #1 with the following polynomials:


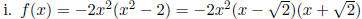
domain for all polynomials is (-∞,∞)
touches: (0, 0); crosses: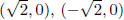
y- intercept is (0, 0)
degree is 4; max number of turning pts is 3
end behavior: as 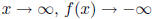, and as

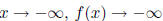
ii. f(x) = -x2(x + 1)(x - 1)
domain for all polynomials is (-∞,∞)
touches: (0, 0); crosses: (1, 0), (-1, 0)
y-intercept is (0, 0)
degree is 4, max number of turning pts is 3
end behavior: as 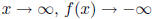, and as

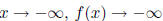
iii. f(x) = x - x3 = x(1 - x2) = x(1 - x)(1 + x)
domain for all polynomials is (-∞,∞)
touches: (0, 0); crosses: (1, 0), (-1, 0)
y-intercept is (0, 0)
degree is 3, max number of turning pts is 2
end behavior: as 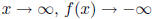, and as

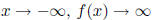
Be able to graph a rational function .

3. Let .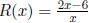

a. (2 pts) What is the domain of R(x)?
b. (2 pts) Identify any x-intercept(s), if there are any. If so, write them as
ordered pairs (x, y).
c. (2 pts) Identify the y-intercept, if there is one. If so, write it as an ordered
pair (x, y).
d. (2 pts) Find the equation(s) of the vertical asymptotes.
e. (3 pts) Find the equation of the horizontal/oblique asymptote.
f. (3 pts) Determine whether the graph of R(x) intersects the horizon-
tal/oblique asymptote.
g. (6 pts) Use the above information and additional test points (as needed)
to sketch the graph of p(x). These points should be labeled on your graph.
Neatness counts!

4. Repeat steps a-g in #3 with the following rational functions:

i.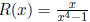
HA is y = 0

ii.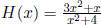
HA is y = 3. Don't worry about this one.

iii.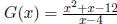
domain is all real numbers except x = 4.
to find the x-intercepts, set y = 0, so we solve 0 = x2+x-12 = (x+4)(x-3),
giving us (-4, 0) and (3, 0).
to find the y-intercept, set x = 0, so we have 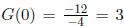, giving us
(0, 3).

VAs are x = 4 (what makes the denominator equal to zero)
Since the degree of the numerator is 1 larger than the degree of the denomi-
nator, we have an OA, which we find by synthetic division, giving us an OA
of y = x + 5.

To find out if the graph of G(x) intersects the OA, we solve the equation :
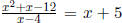. Simplifying , we obtain the statement -20 = -12. This
statement is never true, so it never crosses.

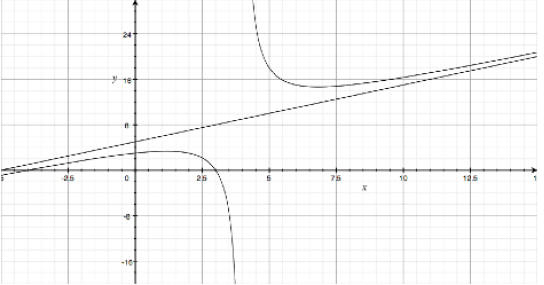
Above, I have the graph of G(x) along with the OA. My graphing utility
won't allow me to draw the VA, but you can see how it will be x = 4.



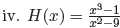
Be able to solve polynomial and rational inequalities .

5. Solve the following inequalities:



Be able to use the Remainder Theorem to find the remainder
when f(x) is divided by x - c. Then use the Factor Theorem to
determine whether x - c is a factor of f(x).

6. Do the above for the following polynomials:

a. f(x) = -4x3 + 5x2 + 8; x + 3, SOLN IS R = 161, not a factor.
b. f(x) = 2x6 - 18x4 + x2 - 9; x + 3, SOLN IS R = -220, not a factor.
c. f(x) = x6 - 16x4 + x2 - 16; x + 4, SOLN IS R = -340, not a factor.

Be able to find all the real zeros of a polynomial function.

7. Find all the real zeros of f(x) = x4 - x3 + 2x2 - 4x - 8.

a. What is the maximum number of real zeros? SOLN: 4
b. Use Descartes' Rule of Signs to determine how many positive and how
many negative real zeros f(x) may have.... SOLN IS 3 or 1 positive real
zeros, 1 negative real zero.
c. List the potential rational zeros.

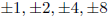
d. Show that -1 is a zero using synthetic division.
After doing the division, you get the depressed eqn x3 - 2x2 + 4x - 8
e. Show that 2 is a zero using synthetic division.
After doing the division, you get the depressed eqn x2 + 4
f. Find all remaining real zeros, if any.
Solve x2 + 4 = 0, giving us .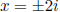

Be able to find the real and complex zeros of a polynomial func-
tion.

8. Let f(x) = x3 - x2 + 9x - 9.

a. What is the number of zeros (real & complex)? SOLN: 3
b. Use Descartes' Rule of Signs to determine how many positive and how
many negative real zeros f(x) may have. SOLN: 3 or 1 positive real zeros,
no negative real zeros.
c. List the potential rational zeros: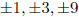
d. Show that 1 is a zero using synthetic division.
Get the depressed eqn x2 + 9 after doing the division.
e. Find all remaining zeros, if any: SOLN is .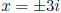
f. Write f in its factored form, as a product of linear factors. (Each factor
is of the form x - c.)
f(x) = (x - 1)(x - 3i)(x + 3i)

9. Repeat a-f of #8 with the following polynomials:

a. f(x) = x4 - x3 + 2x2 - 4x - 8, zeros -1 and 2.

After performing synthetic division with -1, we obtain the depressed equa-
tion (the polynomial at the bottom of the synthetic division) x3-2x2+4x-8.
Now we'll do synthetic division on this polynomial with the other zero 2.
After this round of synthetic division, we get the depressed equation x2 +4.
We can find the zeros of this polynomial either by using the quadratic formula
OR by the following method:



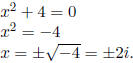
b. f(x) = x3 - 1 = (x - 1)(x2 + x + 1). Then use the quadratic formula
to find the remaining zeros, which are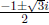

c. f(x) = x4 - 1. Start o factoring as a difference of two squares:
x4-1 = (x2-1)(x2+1) = (x-1)(x+1)(x2+1) = (x-1)(x+1)(x-i)(x+i).

d. f(x) = 2x3 - 5x2 + 6x - 2, zero 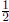. After diving f(x) by ,
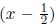we get the depressed equation 2x2 -4x+4 = 2(x2 -2x+2). Again we will
use the quadratic formula to find the remaining zeros of f(x), which are 1+i
and 1-i. The factored form of f(x) = 2(x- 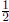)(x-(1+i))(x-(1-i)), or
f(x) = (2x - 1)(x - (1 + i))(x - (1 - i)).

e. f(x) = x4 + 13x2 + 36 Hint: This can be factored! Let y = x2, and
then factor. Then substitute back and find the roots .)
You can write f(x) = (x2 + 9)(x2 + 4) = (x - 3i)(x + 3i)(x - 2i)(x + 2i)

10. Form a polynomial f(x) with real coefficients having the given degree
and zeros.

a. Degree 4, zeros: 2, -i, -i
f(x) = (x - 2)(x2 + 1) then multiply.
b. Degree 6, zeros i, 3 - 2i, -1 + i. SOLN: done in class.
c. Degree 5, zeros 1 of multiplicity 3, 1 + i.
f(x) = (x-1)3(x-(1+i))(x-(1-i)) = (x-1)3((x-1)-i)((x-1)+i) =
(x - 1)3((x - 1)2 - (i)2) = (x - 1)3(x2 - 2x + 2), then multiply once more.

Be able to find a composite function and its domain, verify that
two functions are inverses, find an inverse function.

11. Let 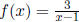and .

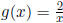Find the following compositions and find the domain of each composite func-
tion.

a. 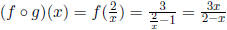Domain is all real numbers except x = 0
and x = 2.

b. 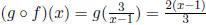Domain is all real numbers except x = 1.

c. 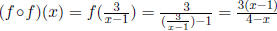Domain is all real numbers except
x = 1 and x = 4.

d. 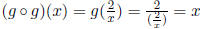Domain is all real numbers except for x = 0.
By the way, this shows us that g is its own inverse!

12. Let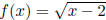 and g(x) = 1 - 2x

Find:

a. 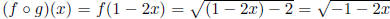We then solve the
inequality -1-2x ≥0 to find the domain. In interval notation, the domain
is 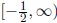. There is no restriction on the domain of the "guy" that we plug
into f because its domain is (-∞,∞).

b. 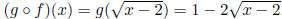. Domain is [2,∞).

c. (f o f)(x) = f(1 - 2x) = 1 - 2(1 - 2x) = 1 - 2 + 4x = -1 + 4x
Domain is  (-∞,∞).

d. 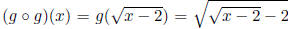. This is interesting, because we
have a couple of restrictions: first, x-2 ≥0, second, we have .
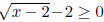Solving the first, we obtain the interval [2,∞), and to solve the second we
do the following: 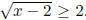. Squaring both sides, we get x - 2 ≥4, and
adding two to both sides, we have x ≥6. So the other interval is [6,∞).
The intersection of [2,∞) and [6,∞) is [6,∞), so this is the domain.

13. Verify that f(x) and g(x) are inverses of each other. This means, you
need to show that (f o g)(x) = x and (g o f)(x) = x.



14. The function f is one-to-one (you should be able to say why if I ask
you!). Find its inverse and check your answer (see above). State the domain
and the range of f and f -1.

a. f(x) = x3 - 1
The cubic function passes the Horizontal Line Test , so it is one-to-one.
Therefore, it's inverse exists.

To find f -1, we interchange x and y, and solve for y:
x = y3 - 1
x + 1 = y3, now take the cube root of both sides (you don't need to take
plus/minus)

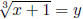
So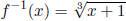
domain and range for both f and f -1 is (-∞,∞).

b. f(x) = x2 + 4, for x ≥0
First of all, not that this function is half of a parabola, which is one-to-one.
Thus, the inverse exists. Since x ≥0,.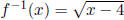
Domain for f is [0,∞), and range is [4,∞). Thus the domain for f -1 is
[4,∞), and range is [0,∞).


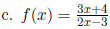
This function is one-to-one. It's inverse is 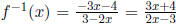. Don't
worry about the domain and range part for this one, and the next one.

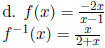
Prev Next