Matrix Operations
1. What size is this matrix?
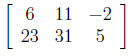
(a) 2x3
(b) 3x2
(c) 6
2. Let
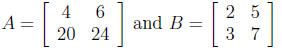
What is A + B?
(a) 71
(b)
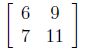
(c)
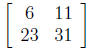
(d)
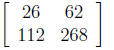
(e)
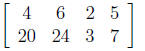
3. If
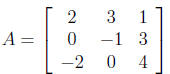what is AT ?
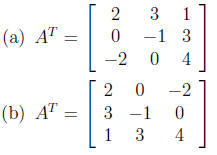
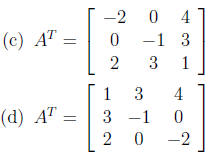
4. If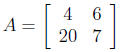 
what is 5A?
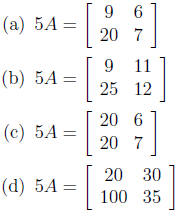
5. If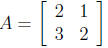 
and
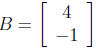then calculate the product AB.
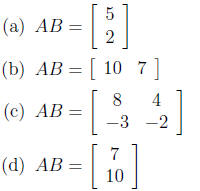
(e) None of the above.
(f) This matrix multiplication is impossible .
6. If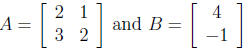
then calculate
the product AB .
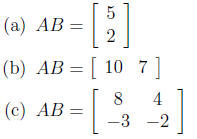
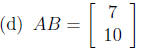
(e) None of the above.
(f) This matrix multiplication is impossible .
7. Calculate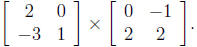 
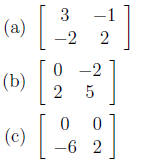
(d) None of the above.
(e) This matrix multiplication is impossible .
8. Calculate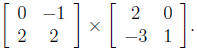 
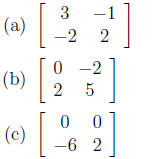
(d) None of the above.
(e) This matrix multiplication is impossible .
9. True or False If A and B are square matrices with the
same dimensions, then (A +
B) (A + B) = A2 + 2AB + A2 .
10. If A and B are both 2x3 matrices, then which of the following is not defined?
(a) A + B
(b) ATB
(c) BA
(d) ABT
(e) More than one of the above
(f) All of these are defined.
11. If A is a 2x3 matrix and B is a 3x6 matrix, what size
is AB?
(a) 2x6
(b) 6x2
(c) 3x3
(d) 2x3
(e) 3x6
(f) This matrix multiplication is impossible.
12. In order to compute the matrix product AB, what must
be true about the sizes of A
and B?
(a) A and B must have the same number of rows .
(b) A and B must have the same number of columns .
(c) A must have as many rows as B has columns.
(d) A must have as many columns as B has rows.
13. If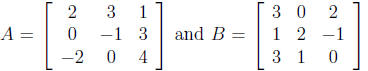 
what is the
(3,2)-entry of AB? (You
should be able to determine this without computing the entire matrix product .)
(a) 1
(b) 3
(c) 4
(d) 8
14. You have a business that sells tables and chairs. You
have brown tables and white
tables, and corresponding chairs. Your May sales are 4 brown tables, 6 white
tables, 20
brown chairs, and 24 white chairs, which is represented by the matrix
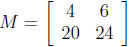
where the first row is tables, the second row is chairs, the first column is
brown items,
and the second column is white items. If your October sales are 50% more than
your
May sales, which of the following would represent your October sales?
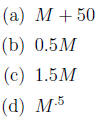
15. You have a business that sells tables and chairs. You
have brown tables and white
tables, and corresponding chairs. Your May sales are 4 brown tables, 6 white
tables, 20
brown chairs, and 24 white chairs, which is represented by the matrix
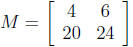
where the first row is tables, the second row is chairs, the first column is
brown items,
and the second column is white items. Your June sales are given by the analogous
matrix J, where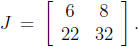 
Which of the following
matrix operations would
make sense in this scenario? Be prepared to explain what the result tells you.
(a) M + J
(b) M - J
(c) 1.2J
(d) MJ
(e) All of the above make sense.
(f) More than one, but not all, of the above make sense.
16. You have a business that sells tables and chairs. You
have brown tables and white
tables, and corresponding chairs. Your May sales are 4 brown tables, 6 white
tables, 20
brown chairs, and 24 white chairs, which is represented by the matrix
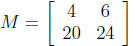
where the first row is tables, the second row is chairs, the first column is
brown items,
and the second column is white items. All tables cost $350 and all chairs cost
$125,
which we represent with the cost vector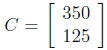 
Which of the following matrix
operations could be useful in this scenario? Be prepared to explain what the
result
tells you.
(a) MC
(b) CM
(c) CTM
(d) MCT
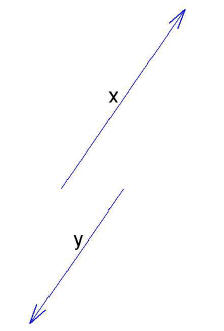
17. True or False Given the vectors x and y plotted
below and some matrix A, if we
know that Ax = 0, this means that Ay = 0 as well.
18. Given the vectors x, y, u, v, and w plotted below and
some matrix A, if we know that
Ax = u, what does this tell us about the product Ay ?
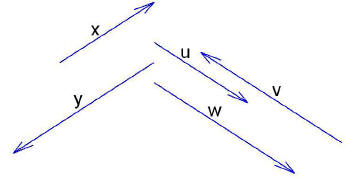
(a) Ay = u
(b) Ay = v
(c) Ay = w
(d) We cannot say anything about Ay without knowing more about A.
| Prev | Next |