Math Review Preparation for Placement Test-Numerical Part
Performing Arithmetic with Measurements:
• Add like units
Example: Add. 4 ft.6in. + 7 ft.10in. = 11 ft.16in. = 12
ft.4in. (16 inches=1 ft. 4 in.)
Subtract. 7lb.5oz. − 3lb.8oz = 3lb.13oz. (When subtracting, borrowing is
sometimes necessary. Change 7 lbs.5 oz. to 6 lbs. 21 oz.)
Multiply. 2qt.1pt.×5 = 10qt.5pt. = 12qt.1pt. (5 pts. = 2 qts. 1 pt.)
Converting from one metric unit to another.
• Use the order of metric conversions:
• kilo, hecto, deka, unit, deci, centi, milli
• km hm dam m dm cm mm
Example:
4200 cm = __________ m. Move two decimal places to the left.
Therefore, the solution is 42 meters.
4.3 L = __________ cL. Move two decimal places to the
right.
Therefore, the solution is 430 cL.
Translating phrases to algebraic expressions :
| • Hints: is, equals, are, results | “=” |
| • sum, plus, increased by, greater than, more than, exceeds, total of |
“+” |
| • difference, minus, decreased by,
less, subtracted from, reduced by, the remainder |
“-“ |
| • product, multiplied, twice, times, of | “x” |
| • quotient, divided by , ratio, per | “ ÷ ” |
| • exponent, power, squared, cubed | “exponent” |
Example:
| 1. a number plus seven results in 10 | x + 7 = 10 |
| 2. the sum of a number and two | x + 2 |
| 3. seven subtracted from five | 5 - 7 |
| 4. three less than a number | x - 3 |
| 5. twice a number | 2x |
| 6. the ratio of five to nine | 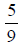 |
| 7. two cubed | 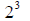 |
| 8. a number to the fifth power | 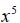 |
| 9. five times the sum of a number and three | 5(x +3) |
Concept #6: Sets of Numbers
Integers
• All positive and negative whole numbers and zero
• Examples: -100, 20, 0, -321, -1, 45
Rational Numbers
• All terminating or repeating decimals
• Examples:
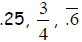
Irrational Numbers
• All non-terminating, non-repeating decimals
• Examples: 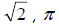
Prime Numbers
• Positive integer greater than 1 with no factors other than itself and 1
• Examples: 5, 17, 29, 41
Real Numbers
• The numbers that can be plotted on a number line.
• Example: 5/3
Absolute Value
• The distance that a number is from zero on a number line.
• Examples: |2| = 2,and |− 5| = 5,and |0| = 0
Concept #7: Operations on Integers
Addition:
• If the numbers have the same sign, add the numbers and take the sign.
• If the numbers have opposite signs, subtract the smaller absolute value
from the larger and attach the sign of the larger .
Examples:
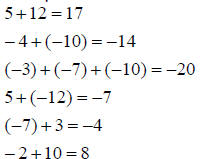
Subtraction:
• Add the opposite of the second number.
Examples:
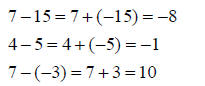
Multiplication and Division
• If the signs are the same, the answer will be positive.
• If the signs are different, the answer will be negative.
Examples:
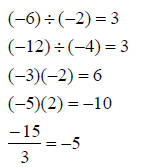
Exponents
• Multiply the base times itself the number of times given by the exponent
Examples:
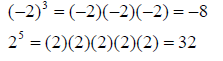
Order of Operations: To evaluate an expression with many
different operations ,
use the following order: P E M D A S “Please excuse my dear aunt Sally”
• P: Parentheses – Start with the innermost symbol, and work outward.
• E: Exponents – Evaluate all exponents.
• M/D: Multiply or Divide – In order from left to right, multiply or divide.
• A/S: Add or Subtract – In order from left to right, add or subtract.
Example:
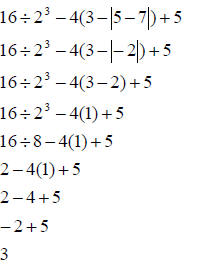
Concept # 8: Algebraic Expressions
Evaluating Algebraic Expressions: To evaluate an algebraic expression with
given
values for the variables:
• Replace every variable with the appropriate real number.
• Use parentheses when substituting a negative number for a variable.
• Use the order of operations to evaluate the resulting expression.
Example: Evaluate y2 − x + 2z + z3 when x = −3, y = −5, and z = 2.
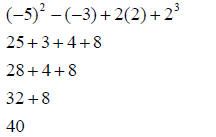
Simplifying Algebraic Expressions
• Starting with the innermost set of parentheses, remove the grouping
symbols. Usually the distributive property and/or rules of exponents must
be used in this step.
• Combine like terms by adding the coefficients of terms having the same
variable factor.
Example: Simplify:
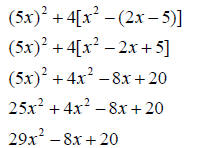
Concept # 9: Ratios, Rates, and Proportions
Ratio: A ratio compares two quantities that have the same
units.
Example: 2 feet to 7 feet
Rate: A rate compares two quantities that have different
units.
Example: 60 miles per hour
Proportion: A proportion is an equation which states that
two ratios or rates are
equal.
Determining the truth of a proportion:
• If the cross products are equal , then the proportion is true.
Example: Is 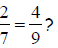 The cross
products would be 2 x 9 = 18 and 4 x 7 = 28.
The cross
products would be 2 x 9 = 18 and 4 x 7 = 28.
Therefore, the proportion is not true since 18 does not equal 28.
Solving Proportions:
• Find the cross products.
• Divide by the number beside the variable.
Example: Solve
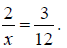
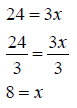
Concept # 10: Linear Equations
Solving Linear Equations :
• Remove all parentheses.
• Add like terms on separate sides of equation.
• Move all variables by adding or subtracting to one side.
• Move all constants by adding or subtracting to other side.
• Isolate the variable by performing the same operation on both sides of the
equation.
Example:
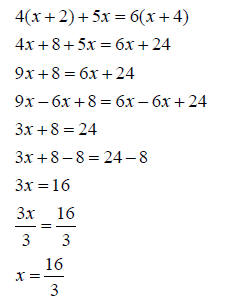
Solving application problems using a linear equation:
• Write verbal equivalence containing the quantities involved in the problem.
• Substitute given values for known quantities.
• Use a variable to represent the unknown quantity .
• Solve the resulting equation.
• Answer the original question.
Example: A person has 90 coins in quarters and dimes with
a combined value of
$16.80. Determine the number of coins of each type.
Value of quarters + Value of dimes = total value
.25(# of quarters) + .10(# of dimes) = 16.80
.25x + .10(90-x) = 16.80
.25x + 9 - .10x = 16.80
.15x + 9 = 16.80
.15x + 9 – 9 = 16.80 – 9
.15x = 7.80
x = 52
So, there were 52 quarters and 90-52 = 38 dimes.
Concept # 11: Exponents
Positive integer exponent: This number indicates how many
times the base is to be
multiplied.
Example:
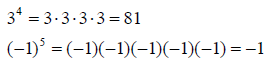
Negative integer exponent: If this number is applied to a
base, it is equal to the
reciprocal of the base raised to the opposite exponent.
Example:
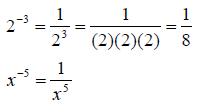
Zero exponent: If this is applied to any base (except 0),
the resulting answer will
be 1.
Example:
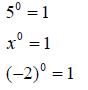
Fractional Exponent: This indicates that a radical should
be applied to the base.
The numerator of the exponent denotes the power to which the base is
raised, and the denominator of the exponent denotes the root to be taken.
Example:
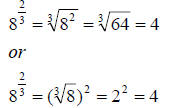
Moving Factors: A factor can be moved from the numerator
of a fraction to the
denominator (or vice versa) by changing the sign of the exponent.
Example:
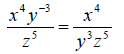 Notice how the “y”
factor was moved to the
Notice how the “y”
factor was moved to the
denominator by changing the -3 to a positive 3.
More examples of exponents:
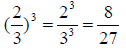
and
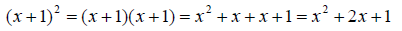
and
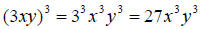
and
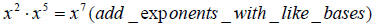
and
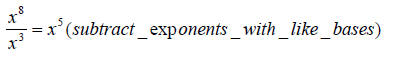
Practice Problems
The answers will follow each section of practice problems.
Whole Number Practice
1. Round to the given place.
a.) 3973 to hundreds
b.) 253687 to ten-thousands
2. Add
a.) 68421 + 985 + 6711
b.) 77 + 886 + 32785 + 8
3. a.) Subtract 4867 from 5223
b.) 5820 minus 625 equals what number?
c.) Find the difference between 7042 and 6134.
4. Multiply
a.) 7024 x 352
b.) 7432 x 504
5. Divide
a.) 30572 ÷ 15
b.) 98521 ÷ 762
6. Evaluate each expression using the order of operations.
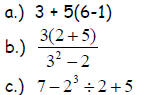
| Prev | Next |