Miscellaneous Math Topics

4 Equation of a Line

A line is identified either by knowing any two points on the line or by knowing
one point and the slope (steepness) of the line.

We usually use Cartesian coordinates to plot lines . y is the vertical axis and
extends infinitely up ( positive ) and down ( negative ). x is the horizontal axis and
extends infinitely left (negative) and right (positive). A point is represented by
a pair of numbers (x,y) that provides its horizontal and vertical location. There
is only one possible line that passes through any two points.

The slope of a line is its ratio of vertical to horizontal change (“rise” over
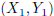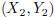“run”). More formally, if and are points on a line, the slope
is:

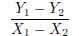
The order of the points does not matter as long as you are consistent and use
the same order for both the numerator and denominator . For any two points on
a line you will get the same slope. The slope is often represented by the letter
m.

Excluding horizontal and vertical lines, every line crosses both axes some-
where. The point where a line crosses the y-axis is called the y- intercept and is
often represented by the letter b. The point where it crosses the x-axis is called
the x-intercept. Horizontal lines cross the y-axis but not the x-axis and vertical
lines cross only the x-axis.

Every line can be expressed by a simple equation in terms of x and y. Point
slope form is a common form for the equation of a line:

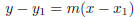
x and y are variables representing the points on the line, is any point
on the line, and m is the slope. For example:

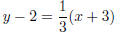
This is the line through the point (−3, 2) with the slope . Another popular
form is the slope-intercept form:

y = mx + b

In this form, x and y are variables and represent some point on the line, m is
the slope and b is the y-intercept. For example, the equation of a line passing
throught the point (1, 2) with slope 3 is:

y = 3x − 1

I found the y-intercept by plugging the coordinates of the point (1, 2) into the
formula : y = 3x + b to get 2 = 3 + b and solving for b. To find another point
on the line, chose a value for x or y and solve for the other coordinate. The y
value when x = 2 is y = 3 * 2−1 = 5 so the line passes through the point (2, 5).

4.1 Exercises: Equation of a line

1. A line passes through the points (1,3) and (2,0). What is the slope? Write
an equation for the line in slope-intercept form. What is the y-intercept?
What is the x-intercept?

2. A line has slope 2 and x-intercept 3. Write an equation for the line.

5 Solutions to Exercises

1.2 Notation

1. [−∞, 2]

2. 3

1.3 Lists

1. 30

1.4 Addition and Multiplication

1. 30

2. 120

3. 0

1.6 The Factorial

1. There are 3! ways. 3! = 3 * 2 * 1 = 6.

2. There are 4(3!) ways. 4 * 3! = 24

3. There are 3! ways to order the methods books and 4! ways to order the
theory books. There are 2 ways to put the books on the shelf (theory
on the left and methods on the right or vice versa). This is (3!)(4!)(2) =
(6)(24)(2) = 288.

2.1 Exponents

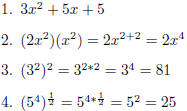
2.2 Logarithms

1.
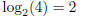
Check this: 2² = 4

2.
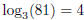
Check this: 3⁴ = 81

3.1 Polynomials

1. The order of 3x⁴ + 18x − 21 is 4.

2. (3x⁴ + 18x − 21) + (2x³ + 3y² − 9x + 6) = 3x⁴ + 2x³ + 3y² + 9x − 15

3.2 Solving Polynomials

Find x in the equations below:

1. 2x − 4 = 0; x = 2

2. x² − 5x − 6 = 0 = (x − 6)(x + 1), x = 6 or x = −1

3. 3x² − 10x + 7

Plug this into the quadratic formula :

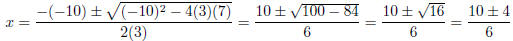
So, 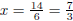or
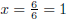
Check this: 3(1²) − 10(1) + 7 = 0. Check 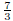yourself.

4.1 Equation of a line

1. First, find the slope: 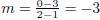or 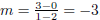. Now we have most
of the equation: y = -3x + b. Second, find the y-intercept by plugging in
one of the points: (3) = (−3)(1)+b; b = 6. Check this by plugging in the
other point: 0 = (−3)(2) + 6 = 0. The equation is y = -3x + 6.

2. We know the slope, so we have y = 2x+b. The x-intercept is 2 so the line
passes through the point (2,0). Plugging in this point gives: 0 = 2(2) + b
so b = −4 and the equation is y = 2x − 4.