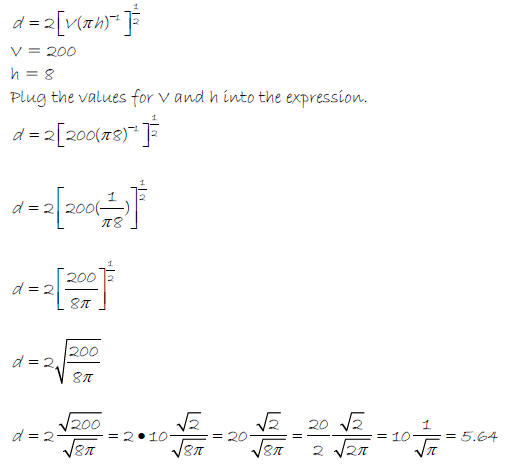Using Powers - Fractional Exponents
Using Powers – Fractional Exponents
Day 1
Warm-up
Solve
1. Find the surface area and volume of a sphere with radius r = 4cm.

2. Evaluate and round to the nearest tenth: x5 when x = 1.3.
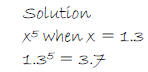
Negative Exponents
Complete the table
| Negative Exponent | Decimal | Fraction |
| 2-1 | 1/2 | |
| 2-2 | 1/4 | |
| 2-3 | 1/8 | |
| 2-4 | 1/16 | |
| 2-5 | 1/32 |
Using the information from the table, draw a conclusion about negative exponents.
Negative Exponent Rule
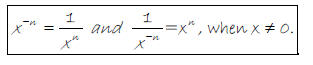
Example 1 – Simplify and write answers with positive
exponents.
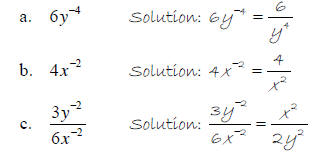
Zero Exponent
Complete the table
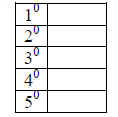
What can we say about x0?
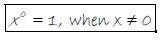
Example
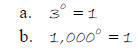
Example 2 – Simplify and write answers with positive exponents .
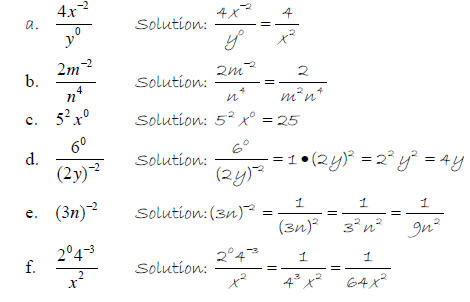
When the exponent is positive, leave it alone!
When the exponent is negative, move it and make it positive!
Homework
• Read pg. 99 - 102
• Pg. 102 #1-10, 39-42
• Pg. 642 Skill 11 evens
• Pg. 642 Skill 12 odds
Day 2
Warm-up
Simplify
1. (5m-6 )(10n2 )
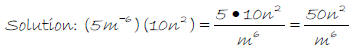
2.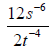
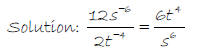
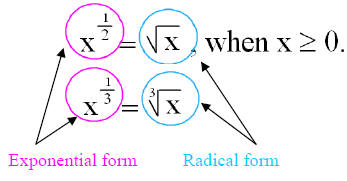
Fractional Exponents and Radical Form
Find
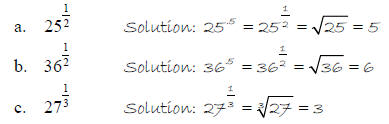
Therefore,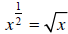 ,when
x 0 and
,when
x 0 and
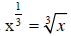 .
.
Example 1 - Rewrite in radical form
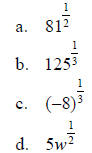
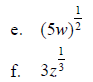
Example 2 – Rewrite in exponential form
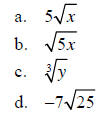
Example 3 – Find the value of each expression when x = 8 and y = 9.
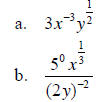
Example 4 – Suppose a roller coaster car can travel at a
speed of 30 ft/s. What would be
the greatest radius of a vertical loop of a track it could make?
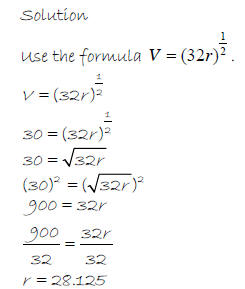
The radius of the track would be about 28 ft.
Example 5 – The diameter of a cylinder with volume V and
height h is given by the
expression
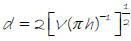 .
.
Find the diameter, to the nearest tenth, of a cylinder
with volume 200 cm3 and height 8
cm.
The diameter is about 5.6 cm.
Review – Write an equation to represent each situation.
Use k to represent the variation
constant.
a. The amount of clay needed to make a square pyramid with
height 1 ft. varies
directly with the square of the length of a base edge.
Solution
V = ke2, where V = amount of clay and e = the base edge.
b. The time it takes to fill a spherical balloon is
directly proportional to the cube
of the radius of the balloon.
Solution
t = kr3, where t = time and r = the radius of the balloon.
Homework
• Read pg. 99 - 102
• Pg. 102 #12-29, 32, 34, 36
• Practice 14 #9-26
| Prev | Next |