More Expressions Involving Rational Exponents

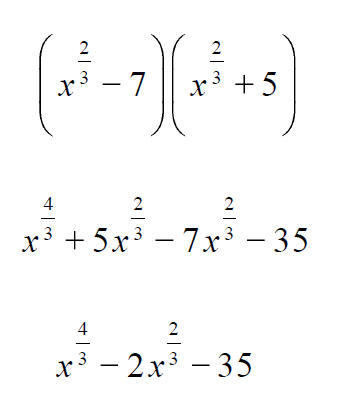
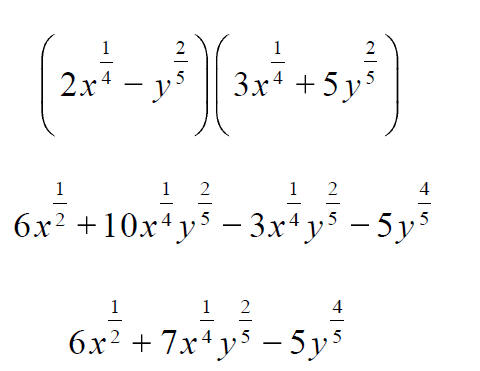
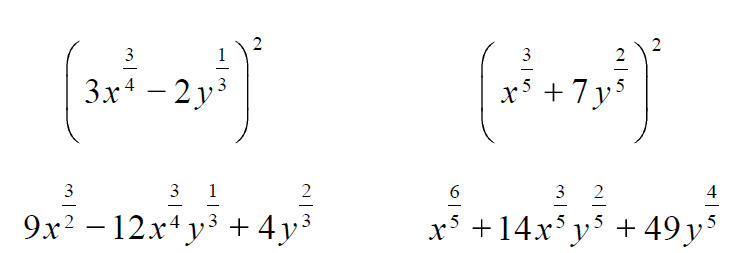
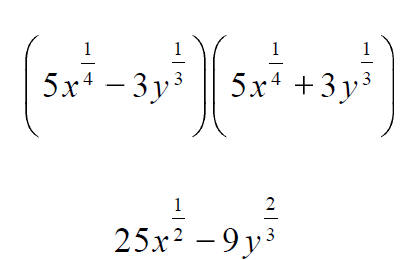
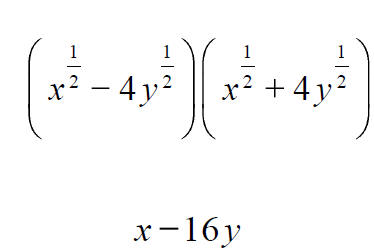
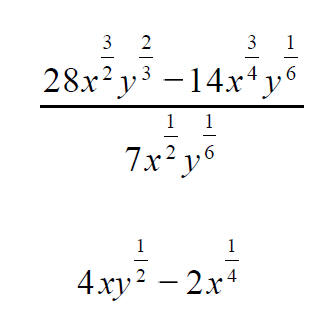
7.3 Simplified Form of Radicals

Simplifying radicals that are not rational .

A radical will be in simplified form when:

1.All factors under the radical sign have exponents that are less than the index.

2.There are no fractions under the radical sign.

3.There are no radicals in the denominator .

Two more rules to remember when playing with radicals:

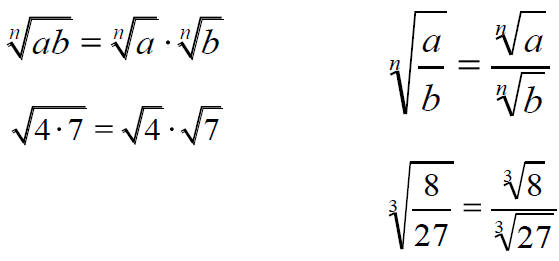
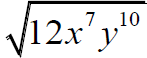	The exponents are to be divided by 2.
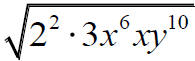	Factor and rewrite the expression so that all exponents aredivisible by 2 or are less than 2. Remove all of the factors with exponents that are 2 or more and divide the exponents by 2.
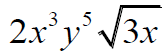	This is simplified form.
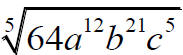	The exponents are to be divided by 5.
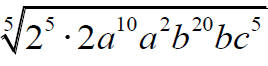	Factor and rewrite the expression so that all exponents are divisible by 5 or are less than 5.
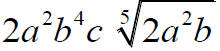	Remove all of the factors with exponents that are 5 or more and divide the exponents by 5.
	This is simplified form.

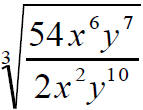
If the expression under the radical can be reduced it will usually
save work if it is reduced at the beginning.

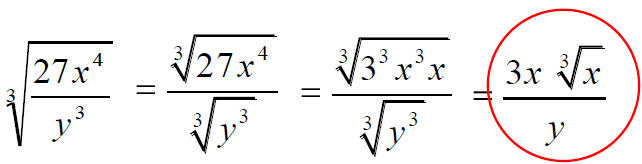
This is simplified form.

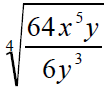	Reduce
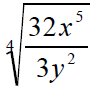	Factor so that all exponents are divisible by 4 or less than 4
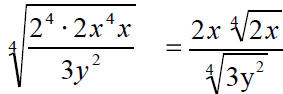	This is almost simplified. The denominator needs to be rationalized.
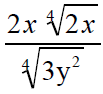	To rationalize the denominator , multiply by 1. Find a way to write 1 so that the exponents in the denominator will be the same as the index
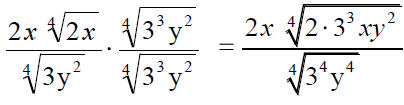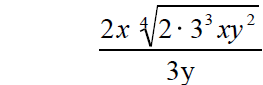	This is simplified form.
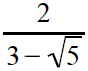	Rationalize the denominator .
	Multiply by one using the conjugate of the denominator.
	At last it is simplified.