Multiplying Polynomials
What does 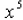 mean?
mean?
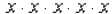
So what is 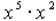 ? Well, it would be
? Well, it would be
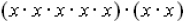 or
or 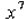 . Now
look back at the
. Now
look back at the
exponents. When you add 5 and 2 the result is 7, right? This is the first rule
of exponents:
*When multiplying like bases , add exponents. (ex.
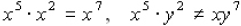 )
)
Ex. 1
Simplify :
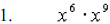 |
*Since the bases are the same, I can add the
exponents and get 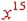 |
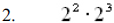 |
*Again, the bases are the same so add the exponents
and get 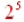 . A . Acommon mistake here is to multiply the 2s and get 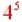 . This is incorrect, . This is incorrect,only add the exponents, don't multiply the bases. |
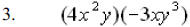 |
*Don't let this one throw you just because it has
more factors . Multiply the coefficients as you normally would and only add the exponents on the like bases . So the answer is 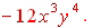 |
Ex. 2 (Monomial times a polynomial )
Multiply:
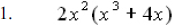 |
We’ll use the distributive property :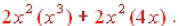 Now it’s just a matter of multiplying monomials and the answer is 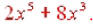 |
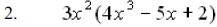 |
Again we’ll use the distributive property: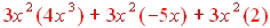 and the answer is and the answer is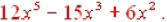 |
Ex. 3 ( Binomial times a binomial)
Multiply:
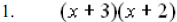 |
There are two methods that we can use here. First, we
can use the distributive property by breaking that first binomial into two monomials:  That will That willgive us  or or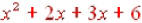 . Notice that the two inside terms
are . Notice that the two inside terms
arelike so we combine those and get 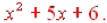 The
other The
othermethod used to multiply binomials is the FOIL method. This is an acronym that stands for First Outside Inside Last. This is the order in which you multiply. First represents the first term in each binomial: x(x). Outside represents the terms on the outside of each binomial: x(2). Inside represents the terms on the inside of the binomials: 3(x). And Last represents the last term in each binomial: 3(2). When we multiply using the FOIL method we get 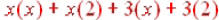 which also gives us which also gives us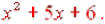 |
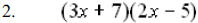 |
Whether you use the distributive property or the FOIL method, you should get: 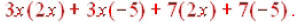 That gives us That gives us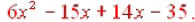 And again, combining the And again, combining theinside terms gives us 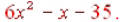 |
Ex. 4 (Binomial times a trinomial )
Multiply:
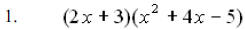 |
Here again we have to use the distributive property: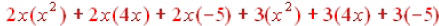 When we multiply, we get 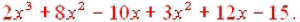 And combining And combininglike terms gives us our answer: 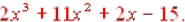 |
| Prev | Next |