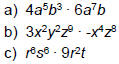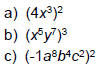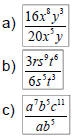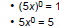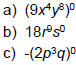Non-negative Exponents

Overview

• Section 5.1 in the textbook:
– Review of exponential notation
– Using the Product Rule
– Using the Power Rule
– Further applications of the Power Rule
– Using the Quotient Rule
– Expressions Raised to the 0 Power

Review of Exponential
Notation

Review of Exponential Notation

• Consider 3⁴ What is its expanded form?
• Consider (-3)⁴ What is its expanded form?
• What about -3⁴?
• What about (½)³?
• Recall an exponential expression is made
up of a base raised to a power
– x^a = x · x · x · x · x · x · x · … · x (a times)
– Identifying the base is the key

Using the Product Rule

Product Rule

• Consider x⁴ · x⁵ How does this expand?
x·x·x·x · x·x·x·x·x
x⁹
• Product Rule: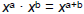

–When multiplying LIKE BASES (the same
variable ), add the exponents

– Only applies when the operation is
multiplication

Product Rule (Example)

Ex 1: Simplify:

Using the Power Rule

Power Rule

• Consider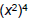

How does this expand ?

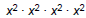x⁸ (using the Product Rule)

• Power Rule: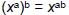

–When raising variables to a power, multiply
the exponents
– Only applies when the exponent is outside a
set of parentheses

PRODUCT Rule versus POWER
Rule

• Be careful not to confuse:
– Product Rule: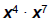

( multiplying LIKE
bases )
– Power Rule: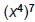

(exponent appears with
NO base)
– It is a common mistake to mix up the
Product Rule and the Power Rule!

Power Rule (Example)

Ex 2: Simplify:

Quotient Rule

Quotient Rule

• Consider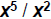

How does this expand?
x·x·x·x·x / x·x
x³

• Quotient Rule: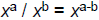

–When dividing LIKE BASES (the same
variable), subtract the exponents
– Only applies when the operation is division

Quotient Rule (Example)

Ex 3: Simplify:

Expressions Raised to the 0
Power

Expressions Raised to the 0 Power

• Consider x⁰
– As long as x ≠ 0, x⁰ = 1
• Can see this by applying the quotient rule
– x can also be an expression
– Be aware of what the zero power is affecting

Expressions Raised to the 0
Power (Example)

Ex 4: Simplify:

Summary

• After studying these slides, you should know how to do
the following:
– Understand exponential notation
– Evaluate an exponential expression given a value
– Understand and use the product rule
– Understand and use the power rule
– Recognize both powers of products and powers of quotients
– Understand and use the quotient rule
– Understand the meaning of an expression raised to the zero
power
• Additional Practice
– See the list of suggested problems for 5.1
• Next lesson
– Negative Exponents and Scientific Notation (Section 5.2)