Factoring Special Products
Overview
• Section 6.5 in the textbook
– Factoring perfect square trinomials
– Factoring the sum & difference of two squares
– Factoring the sum & difference of two cubes
– Factoring completely
Factoring Perfect Square
Trinomials
Notion of a Perfect Square
• A number n is a perfect square if we can
find an Integer k such that k · k = n
– The same Integer times itself
– Ex: 4 is a perfect square (k = 2)
81 is a perfect square (k = ?)
• A variable is a perfect square if its
exponent is evenly divisible by 2
– Ex:
p4 is a perfect square (4 is divisible by 2)
x3 is NOT a perfect square
Perfect Square Trinomials
• Remember to ALWAYS look for a GCF
before factoring!
• Consider what happens when we FOIL
(a + b)2
(a + b)2 = a2 + 2ab + b2
• a2 comes from squaring a in (a + b)2
• 2ab comes from doubling the product of a
and b in (a + b)2
• b2 comes from squaring b in (a + b)2
Factoring Perfect Square
Trinomials
• To factor a perfect square trinomial, we
reverse the process:
– Answer the following questions:
• Are BOTH end terms a 2 and b2 perfect squares of
a and b respectively?
• Is the middle term two times a and b?
– If the answer to BOTH questions is YES, we can
factor a2 + 2ab + b2 as (a + b) (a + b) = (a + b)2
– Otherwise, we must seek a new factoring
strategy
Ex 1: Factor completely:
a) x2y2 – 8xy + 16y2
b) -4r2 – 4r – 1
c) 36n2 + 36n + 9
Factoring the Sum &
Difference of Two Square
Difference of Two Squares
• Remember to ALWAYS look for a GCF
before factoring!
• 2 terms both of which are perfect squares
• Consider what happens when we FOIL
(a + b)(a – b)
(a + b)(a – b) = a2 – b2
• a2comes from the F term in (a + b)(a – b)
• b2comes from the L term in (a + b)(a – b)
Factoring a Difference of Two
Squares
• To factor a difference of two squares, we
reverse the process:
– Answer the following questions:
• Are both terms a2 and b2 perfect squares of a and
b respectively?
• Is the sign between a2 and b2 a – ?
– If the answer to BOTH questions is YES,
a2 – b2 can be factored to (a + b)(a – b)
– Otherwise, the polynomial is prime
Ex 3: Factor completely:
a) x2 – 64y2
b) 6z2 – 54
• Remember to ALWAYS look for a GCF before
factoring!
• Consider a2 + b2
• Only 3 possibilities for the factoring:
(a + b)(a + b) = a2 + 2ab + b2 ≠ a2 + b2
(a – b)(a – b) = a2 – 2ab + b2 ≠ a2 + b2
(a + b)(a – b) = (a – b)(a + b) = a2 – b2 ≠ a2 + b2
• Therefore, the sum of two squares is PRIME
Ex 4: Factor completely:
2x2 + 128
Factoring the Difference &
Sum of Two Cubes
Sum & Difference of Two Cubes
• Remember to ALWAYS look for a GCF
before factoring!
• Consider (a + b)(a2 – ab + b2)
a(a2 – ab + b2) + b(a2 – ab + b2)
a3 – a2b + ab2 + a2b – ab2 + b3
a3 + b3
• Consider (a – b)(a2 + ab + b2)
a(a2 + ab + b2) – b(a2 + ab + b2)
a3 – b3
• Thus:
a3 + b3 = (a + b)(a2 – ab + b2)
a3 – b3 = (a – b)(a2 + ab + b2)
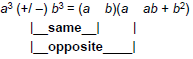
Factoring a Sum or Difference
of Two Cubes
• To factor a sum or difference of two cubes,
we reverse the process:
– Answer the following question:
• Are both terms a3 and b3 perfect cubes of a and b
respectively?
– If the answer is YES, a3 – b3 or a3 + b3 can be
factored into (a – b)(a2 + ab + b2) or
(a + b)(a2 – ab + b2) respectively
– Otherwise, the polynomial is prime
Ex 5: Factor completely:
a) x3 – 8
b) 27y3 + 64z3
c) 250r3 – 2s3
Factoring Completely
• Remember to ALWAYS look for a GCF
before factoring!
• Choose a factoring strategy based on the
number of terms
• Look at the result to see if any of the
products can be factored further
– Polynomials with a degree of 1 or less cannot
be factored further
• e.g. 2x + 1, 7
Ex 6: Factor completely:
a) x4 – 1
b) y4 – 16z4
c) r4t – s4t
Summary
• After studying these slides, you should know
how to do the following:
– Recognize and factor a perfect square trinomial
– Factor a difference of two squares
– Recognize that the sum of two squares is prime
– Factor the difference or sum of two cubes
– Completely factor a polynomial
• Additional Practice
– See the list of suggested problems for 6.5
• Next lesson
– Solving Quadratic Equations by Factoring (Section
6.6)
| Prev | Next |