Roots of Polynomial Equations
Homework:
12.2 #25, 37, 45, 49, 55
12.3 #13b, 15, 19, 35, 45, 55, 57
12.4 #2, 19, 25, 28
Review: An equation is a mathematical statement
that two expressions are
equivalent. A root or solution of an equation is a value (values) such that,
when substituted for the variable (variables) in the equation, the
mathematical statement is true. To solve an equation means to find its
solutions (roots). Equations may have no solutions, a finite number of
solutions , or an infinite number of solutions. Solutions may be real or
complex, single or multiple. We can rewrite an equation in an equivalent
form (i.e., where the solution set is the same) as Expression = 0 .
polynomial equations , roots. The solutions to a polynomial
equation,
an xn + ...+ a1x + a0 = 0, are called the roots of the polynomial. Some
polynomial equations do not have any roots among the real numbers , e.g.,
x2 + 1 = 0 . Some have repeated or multiple roots, e.g., (x - 1)2 = 0 .
Some have distinct roots, e.g., x2 - 1 = 0 . And some have all of the
above, e.g., x2 ( + 1) x2 ( - 1)(x - 1)2 = 0 .
division algorithm for polynomials. The division algorithm
for numbers states that
the dividend is equal to the product of the divisor and the quotient added
to the remainder, where the remainder is less than the divisor
(Dividend = Divisor -Quotient + Remainder ). Similarly, the division
algorithm for polynomials states that f (x) = d(x) · q(x)
+ R(x), where the
degree of the remainder, R(x), is less than the degree of the divisor
d(x). Let f (x) = x3 + 7x2 - x +11 and d(x) = x - 5. Find a polynomial
q(x) and a constant remainder, R(x), such that f (x) = d(x) ·
q(x) + R(x) or
(equivalently)
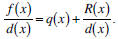
divide polynomials using long and synthetic division . We
can use synthetic
division to divide polynomials when our factor is linear of the form
x - r . Find the quotients and remainders for:
(1) 9x4 + x3 -12x + 21 divided by x + 4
(2) 3r4 +16r3 - 5r +19 divided by 3r - 2
remainder theorem. The division algorithm for polynomials
states that for
linear divisors , x - r, f (x) = (x - r) · q(x) + R(x)
where the degree of the
remainder, R(x), is zero . The Remainder Theorem states when a
polynomial f (x) is divided by x - r , the remainder is f(r). [Substitute r
for x.] What is the remainder when f (x) = x4 - 3x3 + 7x2 - x + 5 is
divided by x - 3? Without substituting, what is f (3)?
(linear) factor theorem. The (Linear) Factor Theorem
states: Let f (x) be a
polynomial. If f (r) = 0, then x - r is a factor of f (x) . Conversely, if x - r
is a factor of f (x) , then f (r) = 0. We know even more. If (x - rk ) is a
factor of f (x) , then:
• f (x) is divisible by (x - rk )
• rk is a zero of f (x) , i.e., f (rk ) = 0
• rk is a root of
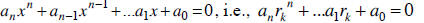
• rk is a x-intercept of the graph of f (x)
The (Linear) Factor theorem can be used to obtain a
reduced equation and,
thus, to find the remaining roots. We divide f(x) by x - r to get f (x) = (x -
r) · q(x), where
q(x) is the quotient function. Since q is one degree less than f, hopefully it
is easier to solve
q(x) = 0 than the original equation
f (x) = 0. Q(x) is called a reduced equation of f. If 3 and -2/3 are
roots of equation 3x4 + 5x3 - 49x2 +11x + 30 = 0, find the other roots.
fundamental theorem of algebra . Does every polynomial
equation of
degree at least 1 have a root ? Or, to pose the question differently, is it
possible to write a polynomial equation that has no solutions? If we allow
only real solutions, then we can easily write an equation with no real roots:
x2 = -1. However, if we allow complex roots, then it turns out that every
polynomial equation has at least one root. This is known as the
Fundamental Theorem of Algebra. This theorem applies not only to
polynomials with rational number coefficients
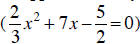 but also to polynomials with real number coefficients
but also to polynomials with real number coefficients
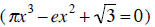 and
with complex number coefficients (x2 - 2ix + [3+ i] = 0).
and
with complex number coefficients (x2 - 2ix + [3+ i] = 0).
linear factors theorem. According to the Fundamental
Theorem of Algebra, the
equation f (x) = an xn + an-1xn-1 + ...+ a1x + a0 = 0 has at least one
(possibly complex) root. Let's call this root r1. By the Factor Theorem,
x - r1, is a factor of f (x) , and we can write f (x) = (x - r1)Q1(x) , where
Q1(x) is a polynomial of degree n -1 and leading coefficient an . If the
degree of Q1(x) is zero, i.e., it is a constant, then were done and
Q1(x) = an . If not then we can write Q1(x) = (x - r2)Q2(x) for a Q2(x) of
degree n - 2 and leading coefficient a n. Continuing this process, we can
write f (x) = an (x - r1)(x - r2)...(x - rn ) . Therefore, a polynomial
equation
of degree n ≥ 1 has exactly n roots (some possibly complex), where some
roots may be repeated (multiple) roots. We can factor
6x2 + x -12 as (3x - 4)(2x + 3). We can find the roots of
6x2 + x -12 = 0 by setting each factor equal to zero. Therefore, the roots are
x = 4/3, x = -3/2. Finally, we write
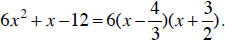 We
can
We
can
also use this theorem to find polynomial functions with given roots. Find
a quartic polynomial with roots
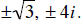
| Prev | Next |