Math 121,Practice Questions for Chapter 2
1. (a) Find the distance between the points (-3, 2) and
(9,-3).
(b) find the midpoint of the line segment with endpoints (3, 5) and (-5, 2).
2. (a) Determine the center and radius of the circle whose
equation is x2+y2+10x+4y+20 = 0.
(b) Write the equation of a circle whose center is (-5, 1) and passes through
the point (3, 1).
(c) Find the equation of a circle that has diametral endpoints of (0, 0) and (6,
8). (Hint: the
center is the midpoint of the diametral endpoints).
3. Let f(x) = 2x2 + 7 and g(x) = |x - 1|, find
(a) (f ◦ g)(-5)
(b) (g ◦ f)(x)
(c) (fg)(0)
(d) (f + g)(0)
4. Let f(x) = 4x2 - 3x, find the difference quotient
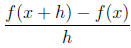
5. Sketch the graph of f (x) = |x + 3| - 2 and find
intervals where f is (a) increasing; (b)
decreasing. Is f one-to-one?
6. Determine the domains of the following functions.
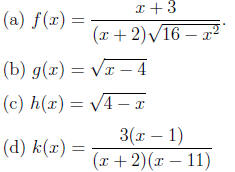
7. (a) Find the slope - intercept form of the line through
the points (-1, 3) and (4,-7).
(b) Find the slope-intercept form of the line that passes through the point
(-3,-7) and is
perpendicular to the line 2x + 5y = 10.
(c) Find the slope-intercept form of the line that passes through the point
(-3,-7) and is
parallel to the line 2x + 5y = 10.
8. (a) Write the quadratic function f(x) = -3x2 + 4x - 5
in standard form by completing the
square . Using that information, sketch the graph of f(x).
(b) Find the vertex of the quadratic function f(x) = 3x2 - 6x+11, and
find the
range of f(x).
(c) Find the maximum of the quadratic function f(x) = -3x2+3x+7 and then
find its
range.
(d) Find the range of the quadratic funciton f(x) = x2 - 10x + 3. Does this
function have a
maximum or a minimum? If so, find it.
9. An air freight company has determined that its cost of delivering x parcels per flight is
C(x) = 875 + 0:75x
and it charges $12.00 per parcel to send each parcel.
Find:
(a) the revenue function;
(b) the pro t function;
(c) the minimum number of parcels the company must ship on a flight to break even.
10. The height in feet of a projectile with an initial
velocity of 64 feet per second and an initial
height of 80 feet is a function of time t in seconds, given by
h(t) = -16t2 + 64t + 80.
(a) Find the maximum height of the projectile.
(b) Find the time t when the projectile reaches its maximum height.
(c) Find the time t when the projectile hits the ground (has a height of 0
feet).
(d) The difference quotient
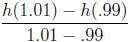gives the average velocity of the projectile for
.99 ≤ t ≤ 1.01. Compute this difference quotient. Do you think it would provide a
good
estimate of the instantaneous velocity of the projectile when t = 1?
11. (a) Do # 41, p. 275.
(b) Determine whether the graph of y = x3 - 4x is symmetric about the (i)
x-axis, (ii) y-axis,
(iii) origin.
(c) Determine whether the function g(x) = x5 - x3 is even, odd or neither.
(d) In terms of shifts or translations, how does the graph of y = f(x + 5) - 10
compare to the
graph of y = f(x)?
(e) In terms of shifts or translations, how does the graph of y = f(x + 5) - 10
compare to the
graph of y = f(x - 3) + 2?
12. Find two numbers whose difference is 10 and the sum of whose squares is a minimum .
13. Let
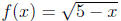and
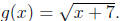Find the domain of (i) f + g, (ii) f - g, (iii) fg,
(iv) f=g.
14. A farmer has $1000 to spend to fence a rectangular
corral. Because extra reinforcement
is needed on one side, the corral costs $6 per foot along that side. It costs $2
per foot to fence
the remaining sides. What dimensions of the corral will maximize the area of the
corral?
15. A Hollywood charter bus company that provides tours
through the movie star neighbor-
hoods in Beverly Hills has determined that the cost of providing x people a tour
is
C(x) = 180 + 2:50x
A full tour consists of 60 people. The ticket price per
person is $15 plus $0.25 for each unsold
ticket. Determine
(a) The revenue function.
(b) The pro t function.
(c) The company's maximum pro t.
(d) The number of ticket sales that yields the maximum pro t.
16. Answer the following in terms of shifts, reflections,
stretching or shrinking.
(a) How does the graph of y = f(-x) relate to the graph of y = f(x)?
(b) How does the graph of y = -f(x) relate to the graph of y = f(x)?
(c) How does the graph of y = -f(x + 2) relate to the graph of y = f(x)?
(d) How does the graph of y = f(5x) relate to the graph of y = f(x)?
(e) How does the graph of y = f( 1/12x) relate to the graph y = f(x)?
(f) How does the graph of y = 10f(x) relate to the graph of y = f(x)?
17. For conceptual graphing questions, see 57; 58; 59; 63; 69; 73 in Section 2.5.
18. (a) The function I(x) = 12x converts feet to inches
and the function F(x) = 5280x
converts miles to feet. Compute (I ◦ F)(x) and explain its meaning.
(b) Let f(x) = x2 + 4x - 1 and g(x) = x + 2. Find f ◦ g and g ◦ f.
(c) Let f(x) = x2 + 1 and
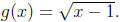Compute f ◦ g and g ◦ f. What are their domains?
Are f ◦ g and g ◦ f equal?
19. Julie opened a lemonade stand and found that daily her
pro t is a linear function of the
number of cups of lemonade sold. When she sells 300 cups of lemonade, she makes
$40 and
when she sells 600 cups of lemonade, she makes $130.
(a) Find the pro t function.
(b) How many cups of lemonade does Julie need to sell to break even on a given
day?
(c) How many cups of lemonade does Julie need to sell to make $100 in a day?
(d) How much would she make on a day when she sells 1000 cups of lemonade?
Further Practice: See Test 2 from Autumn 2004, Winter 2005, Winter 2006, Autumn 2006.
| Prev | Next |