Exponents
Section P.2
Exponential Notation
for Positive Integers
Let b be a real number or a variable
representing a real number. Let n be a
positive integer.
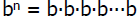where there are n b’s
Example: 
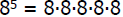
Example:
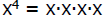
Product Rule for Exponents
What happens to the exponents when
we multiply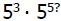 
Solution :
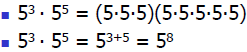
Exponential Rules
We want the Product Rule for
Exponents to hold for
powers that are
not positive integers as well. Determine
the definition of each
of the following
exponential rules by ensuring that the
Product Rule for
Exponents holds.
For any real number a ,
what does 
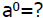
Solution
We want to define a zero power so that
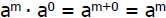
What must a0equal for this to happen?
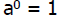
For any real number a,
what does 
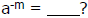
Solution
We want to define a negative power so that
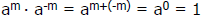
What must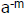 
equal for this to happen?
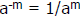so a negative power means
reciprocal
Division Rule for Exponents
For any non-zero real number a, what
does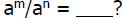 
Solution
Using the rule for negative exponents
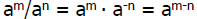
So when we divide expressions with the
same base, we subtract powers.
Other Exponential Rules
Determine the rules for the following by
expanding the
expression .
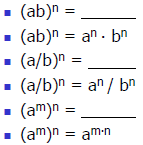
Skills
Use the Exponential Rules to simplify
the following
expressions to a common
form having
Only positive exponents
All like terms combined
Constant portion reduced to lowest terms
Skills Practice
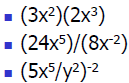
How do we extend the notion of exponents to
the rational numbers? What is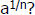 
Solution:
Using the Power to a power rule, examine
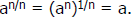So the power 1/n undoes
the power n. What operation undoes
taking
an nth power?
Example: a2 can be undone by taking
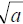that
is .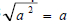
,So we define
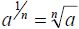
Radical Rules
Simplifying expressions that have
radicals can be done
by converting the
radical to a rational power and then
applying the exponential
rules. Try one
of these three examples.
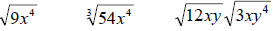
Common simplified form for radical
expressions is
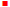All factors removed from radical
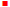Index of radical reduced to lowest terms
Rationalize the denominator (no radical left
in the denominator)
Skills Practice
Simplify the following radical expression
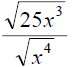
| Prev | Next |