Preparation for Math Chapter 4
1- Synthetic Division
If a polynomial p (x) is divided by (x – c) we can apply synthetic division:
Let’s divide x3 – 4x2 – 5 by x – 3
Step 1: Write the dividend in descending powers of x. Copy the coefficients;
write a zero
for any missing power .
1 -4 0 -5
Step 2: Create the following structure:
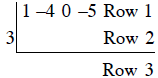
First row, we place: 1 -4 0 -5
Second row, to the left of the symbol , we place 3 since the divisor is x – 3.
Step 3: Bring the 1 down two rows , and enter it in row 3.
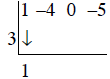
Step 4: Multiply the 1, in row 3, by 3, and place the result 3, in row 2 underneath the -4.
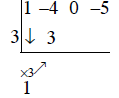
Step 5: Add the entries in row 1 and row 2 (-4 + 3 = -1) and enter the sum in row 3.
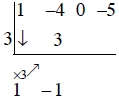
Step 6: Multiply the -1, in row 3, by 3, and place the result -3, in row 2 underneath the 0.
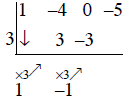
Step 7: Add the entries in row 1 and row 2 (0 + -3 = -3) and enter the sum in row 3.
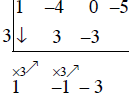
Step 8: Multiply the -3, in row 3, by 3, and place the result -9, in row 2 underneath the -5.
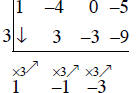
Step 9: add the entries in row 1 and row 2 (-5 + -9 = -14) and enter the sum in row 3.
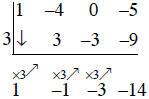
End of the process.
The numbers 1 -1 and -3 are the coefficients of a second degree polynomial that
is the
quotient (x2 – x – 3), the number -14 is the remainder, so
x3 - 4x2 – 5 = (x - 3)(x2 – x – 3) + (-14)
Example:
Use synthetic division to divide (2x5 + 5x4 – 2x3 + 2x2 – 2x + 3) by (x + 3)
The divisor is x + 3 = x – (-3), so we place -3 to the left of the symbol.
Remember, we add each entry in row 1 to the corresponding entry in row 2 and the
sum
is place in row 3.
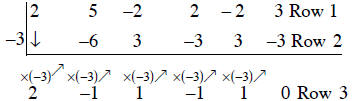
The remainder is 0, the quotient is the polynomial 2x4 –
x3 + x2 – x + 1, so
2x5 + 5x4 – 2x3 + 2x2 – 2x + 3) = (x + 3)( 2x4 – x3 + x2 – x + 1)
2- Roots or Zeros of a Polynomial
Given a polynomial P(x), we say that a number c is a root or zero of the
polynomial if
P(c) = 0.
The Factor Theorem :
The number c is a root or zero of the polynomial P(x) if and only if (x – c) is
a factor of
P(x). (P(x) = (x – c) Q(x) where degree Q(x) equals degree P(x) minus 1)
Example:
Show that x – 1 is a factor of P(x) = 2x3 – x2 + 2x – 3.
Applying the theorem, we have to show that P(1) = 0.
P(1) = 2(1)3 – (1)2 + 2(1) – 3 = 2 – 1 + 2 – 3 = 0
Then P(x) = 2x3 – x2 + 2x – 3 = (x -1)Q(x).
We can find Q(x) using synthetic division,
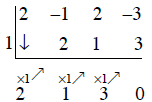
Q(x) = 2x2 – x + 3 and P(x) = 2x3 – x2 + 2x – 3 = (x -1)(
2x2 – x + 3).
3- Quadratic Equation
A quadratic equation has the form : ax2 + bx + c = 0 where a, b, and c are real
numbers.
We can use quadratic formula to find the roots or zeros,
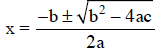
b2 – 4ac is called the discriminat.
If b2 – 4ac > 0, there are two unequal real number solutions.
If b2 – 4ac = 0 there is a repeated solution, root of multiplicity 2.
If b2 – 4ac < 0 there are no real solutions, two distinct complex number
solutions.
4- The Rational Zeros Theorem
Let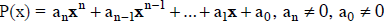 
be a polynomial with integer
coefficients.
A rational number p/q in lowest terms , is a rational zero of P(x) if p is a
factor of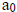 
and q
is a factor of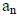 
.
Example:
List the potential rational zeros of P(x) = 2x3 + 11x2 – 7x – 6.
Notice that the coefficients of P(x) are integer numbers.
Since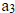 
= 2 and
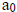= -6, then p is a factor of -6 and q is a factor of 2:
p : ±1, ±2, ±3, ±6 (factors of -6)
q: ±1, ±2 (factors of 2)
Now, we form all possible ratios p/q: ±1, ±2, ±3, ±6, ±1/2, ±3/2. There are 12
possible
candidates. So if P(x) has a rational zero, it is one of those listed. It may be
the case that
P(x) does not have any rational zero.
By substitution , we can check each potential zero, to determine whether it is
indeed a
zero.
Let’s start with 1, P(1) = 2(1)3 + 11(1)2 – 7(1) – 6 = 0. It is a zero, then (x
– 1) is a factor
of P(x).
We can use synthetic division to factor P(x)
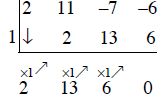
Then, P(x) = (x -1)(2x2 + 13x + 6) = (x – 1)(x + 6)(x +
½), using quadratic formula, so 1,
-6, and -1/2 are the zeros of P(x).
| Prev | Next |