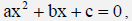Problem Solving: Interest, Mixture, Uniform Motion, Constant Rate Job

1 Conception

You do not need to memorize these conceptions, but make sure you understand them and be
able to solve the problems contain them.

(1) Interest Problem:

Interest
Rate of interest
Simple Interest
Principal

(2) Mixture Problem: note the units of two materials

(3) Uniform Motion Problems:

Uniform Motion
Velocity
Distance

(4) Constant Rate Job Problems

Constant Rate Job

2 Formulas

(1) Simple Interest Formula (p. A63)

(2) Uniform Motion Formula (p. A65)

3 Solve Interest Problem

4 Solve Mixture Problem

5 Solve Uniform Motion Problems

6 Solve Constant Rate Job Problems

A.9 Interval Notation; Solving Inequalities

1 Use Interval Notation

Memorize Table 5 (p. A73), and test yourself by finishing the following form

Interval Type	Interval Notation	Inequality	Sketch the graph
		a<x<b
		a≤x≤b
Half-open	[a, b)	a≤x<b
		a<x≤b
		x≥a
		x>a
		x≤a
		x<a
		All Real Numbers

2 Use Properties of Inequalities

Memorize the following four properties, and fill in the blanks with proper inequality symbols .

(1) Nonnegative Property (p. A73)

For any real number a , a² □ 0.

(2) Addition Property of Inequalities (p. A74)

For real numbers a, b, and c,
If a<b, then a+c □ b+c.
If a>b, then a+c □ b+c.

(3) Multiplication Properties for Inequalities (p. A74)

For real numbers a, b, and c,
If a<b and if c>0, then ac □ bc.
If a<b and if c>0, then ac □ bc.
If a>b and if c>0, then ac □ bc.
If a>b and if c<0, then ac □ bc.

(4) Reciprocal Property for Inequalities

If a>0, then 1/a □ 0. If 1/a> 0, then a □ 0.
If a<0, then 1/a □ 0. If 1/a < 0, then a □ 0.

3 Solve Inequalities

(1) Be familiar with the type of procedures leave the inequality symbol unchanged or reversed.
Fill in the blanks with the proper inequality symbols (<, >, ≤, ≥). (p. 75)

For expressions A, B, C, and D,

If ( A + C ) + B > D, then A + C + B □ D.
If A > B, then A + C □ B + C.
If A > B, then A – C □ B – C.
If A > B and C > 0, then .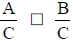
If A > B and C≥0, then A× C □ B× C.
If A > B , then B □ A.
If A > B and C < 0, then .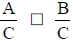
If A > B and C≤0, then A× C □ B× C.

(2) Solve an Inequality

4 Solve Combined Inequalities

5 Solve Inequalities Involving Absolute Value

A.10 nth Roots ; Rational Exponents

1 n-th root

(1) Definition

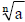
Radical
Index
Radicand
Square root
Cube root

(2) Formula for 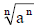(p. A82)

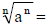, if n≥3 is odd.

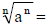, if n≥2 is even.

(3) Using a calculator to approximate n-th root (p. A82)

(4) Properties of Radicals (p. A83)

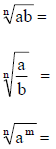
(5) Simplify the radicals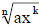

a) Write the coefficient of the radicand as m-th (m≥n) power, i.e.,

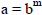
b)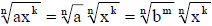

c) Divide m and k by n, we have

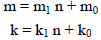
with integers 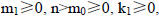and

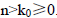
d)
If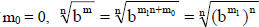

If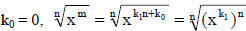

e)
If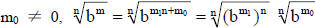
If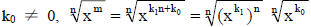

f) Using the formulas in (2) to simplify the term

(6) Combing Like Radicals

Note first simplify then combing. You CANT combine the like radicals as the following

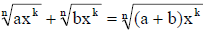(ERROR!)

2 Rationalize Denominators

(1) If the denominator is monomial

a) Simplify the denominator first, and then get a new radical 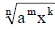(m<n and k<n)

b) Multiply by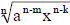

(2) If the denominator is binomial, A±B

Multiply by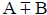

3 Solve Radical Equations

(1) Move the radical to the left side, and the other terms to the right side
(2) Raise each side to the n-th power and solve

4 Simplify expressions with rational exponents

(1) Definition

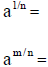
(2) Writing expressions containing Fractional Exponents as Radicals

(3) Simplifying Expressions Containing Rational Exponents
Similar to the polynomial operations

(4) Writing an expression as a single quotient

(5) Factoring an Expression Containing Rational Exponents

A.7 Complex Numbers ; Quadratic Equations
in the Complex Number System

1 Definition (p. A54)

Imaginary unit	i
Complex number	a+bi
Standard form
Pure Imaginary number	bi
Conjugate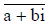
Principal square root

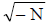2 Formulas (p. A55)

Equality of Complex Number

a + bi = c + di if and only if a = c and b = d

Sum of Complex Numbers

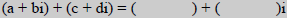Difference of Complex Numbers

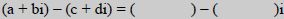Product of Complex Numbers

Powers of i (p. A58)

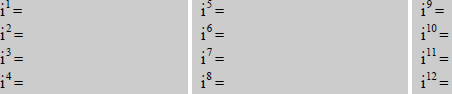3 Theorems (p. A56-A57)

The product of a complex number and its conjugate is a nonnegative real number.

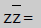The Conjugate of a real number is the real number itself.

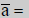The conjugate of the conjugate of a complex number is the number itself.

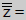The conjugate of the sum of two complex numbers equals the sum of their conjugates.

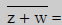The conjugate of the product of two complex numbers equals the product of their conjugates.

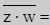Quadratic Formula: In the complex number system, the solution of the quadratic equation

Where a, b, and c are real numbers and a≠0, are given by the formula

4 Add, Subtract , Multiply, and Divide Complex Numbers

(1) Take the imaginary unit i as the square root 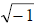or a variable , and then follow the rules of
the operations of the polynomials

(2) Substitute the powers of i with the above formulas (p. A58)

(3) Write in Standard Form

5 Solve quadratic equations in the complex number system