Quadratic Equations
| Quadratic Equations A quadratic equation in x is an equation that can be written in the general form ax2 + bx + c = 0 Where a, b, and c are real numbers We can solve by several methods : • By Factoring and setting each factor equal to 0 • Extracting Square Roots • Completing the Square • Using the Quadratic Formula • Using Your Calculator Wisely |
||||
| Quadratic Equations - Factoring Factor ax2 + bx + c = (Ax+B)(Cx+D) = 0 • Set each factor = 0. (Ax+B) = 0, (Cx+D) = 0 • Solve for x Examples: To be worked in class |
||||
| Quadratic Equations – Extracting
Square Roots • If you can manipulate the equation so that:
then, |
||||
| Quadratic Equations – Completing the
Square Given : 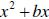 we can make it a " perfect square " we can make it a " perfect square "
|
||||
| Quadratic Equations – The Quadratic
Formula Given :
Examples: To be worked in class |
||||
| Quadratic Equations – Types of
Solutions
|
||||
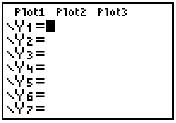
| Quadratic Equations – Solving By
Graphing A function must be entered into  in order to obtain its graph. in order to obtain its graph.Press the  key. The resulting screen should look like this key. The resulting screen should look like this
|
||||
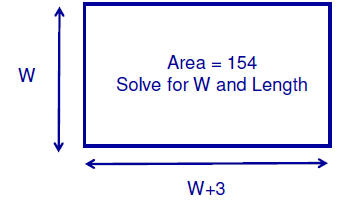 |
||||
 |
235 ft | A Wrench Is Dropped From 235 ft up
|
||
| Number of Lawyers L = .008t2 + 19.59t + 552.8, t = 3 is 1983, L is in thousands, What year does L =1000? (That is 1 million Lawyers?) |
||||
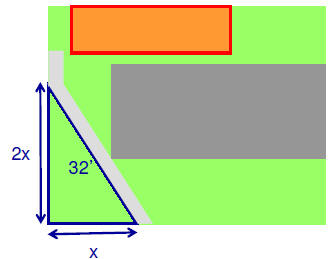
Taking a Shortcut |
||||
| Prev | Next |
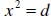
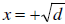 and
and
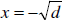 or
or
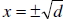
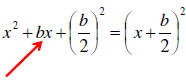
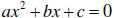 we can use the quadratic formula
we can use the quadratic formula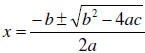
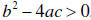 , then there are
, then there are 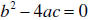 , then there is one
, then there is one 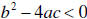 , then there are two
, then there are two 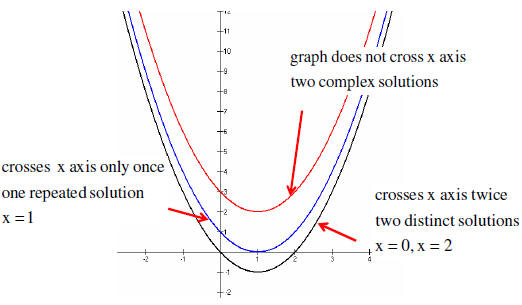
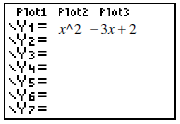
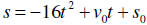
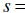 Position from top
Position from top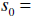 Initial position 235
Initial position 235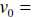 Initial velocity 0 (If it is just dropped)
Initial velocity 0 (If it is just dropped)