SOLUTION OF NONLINEAR EQUATIONS f(x)=0

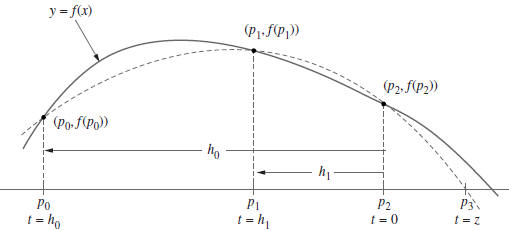
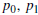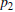Figure 2.17 The starting approximations , and for Muller’s method, and the
differences 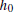and .

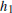Muller’s Method
Muller’s method is a generalization of the secant method, in the sense that it does
not require the derivative of the function. It is an iterative method that requires three
starting points 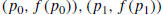, and 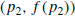. A parabola is constructed
that passes through the three points; then the quadratic formula is used to find a root
of the quadratic for the next approximation. It has been proved that near a simple
root Muller ’s method converges faster than the secant method and almost as fast as
Newton’s method. The method can be used to find real or complex zeros of a function
and can be programmed to use complex arithmetic.

Without loss of generality, we assume that 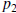is the best approximation to the
root and consider the parabola through the three starting values , shown in Figure 2.17.
Make the change of variable



and use the differences

and .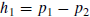

Consider the quadratic polynomial involving the variable t :

(11) y = at² + bt + c.

Each point is used to obtain an equation involving a, b, and c:

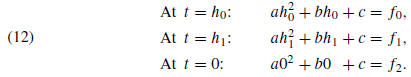
From the third equation in (12), we see that



Substituting (13) into the first two equations in (12) and using the definition
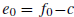
and 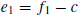results in the linear system

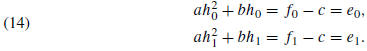
Solving the linear system for a and b results in

The quadratic formula is used to find the roots 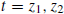of (11):

Formula (16) is equivalent to the standard formula for the roots of a quadratic and is
better in this case because we know that .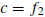

To ensure the stability of the method, we choose the root in (16) that has the smallest
absolute value. If b > 0, use the positive sign with the square root, and if b < 0,
use the negative sign . Then is shown in Figure 2.17 and is given by



To update the iterates, choose the new and the new 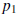to be the two values
selected from among the old 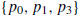that lie closest to 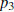(i.e., throw out the one
that is farthest away). Then take new to be old 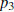. Although a lot of auxiliary
calculations are done in Muller’s method, it only requires one function evaluation per
iteration.

If Muller’s method is used to find the real roots of f (x) = 0, it is possible that
one may encounter complex approximations, because the roots of the quadratic in (16)
might be complex (nonzero imaginary components). In these cases the imaginary components
will have a small magnitude and can be set equal to zero so that the calculations
proceed with real numbers.

Table 2.12 Comparison of Convergences near a Simple Root

k	Secant method	Muller’s method	Newton’s method	Steffensen with Newton

Comparison of Methods

Steffensen’s method can be used together with the Newton-Raphson fixed-point function
g(x) = x − f (x)/ f '(x). In the next two examples we look at the roots of
the polynomial f (x) = x³ − 3x + 2. The Newton-Raphson function is g(x) =
(2x³ − 2)/(3x² − 3). When this function is used in Program 2.7, we get the calculations
under the heading Steffensen with Newton in Tables 2.12 and 2.13. For example,
starting with 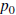= −2.4, we would compute



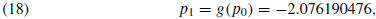
and



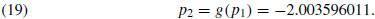
Then Aitken’s improvement will give = −1.982618143.

Example 2.19 (Convergence near a Simple Root). This is a comparison of methods
for the function f (x) = x³ − 3x + 2 near the simple root p = −2.

Newton’s method and the secant method for this function were given in Examples 2.14
and 2.16, respectively. Table 2.12 provides a summary of calculations for the methods.

Example 2.20 (Convergence near a Double Root). This is a comparison of the methods
for the function f (x) = x³ − 3x + 2 near the double root p = 1. Table 2.13 provides a
summary of calculations.

Newton’s method is the best choice for finding a simple root (see Table 2.12). At a
double root, either Muller’s method or Steffensen’s method with the Newton-Raphson
formula is a good choice (see Table 2.13). Note in the Aitken’s acceleration formula (4)
that division by zero can occur as the sequence converges. In this case, the last
calculated approximation to zero should be used as the approximation to the zero of f .

Table 2.13 Comparison of Convergence Near a Double Root

k	Secant method	Muller’s method	Newton’s method	Steffensen with Newton

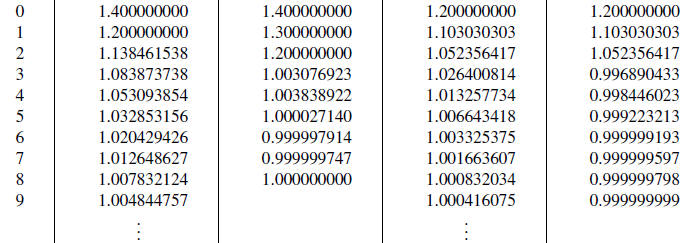In the following program the sequence , generated by Steffensen’s method
with the Newton-Raphson formula, is stored in a matrix Q that has max1 rows and
three columns. The first column of Q contains the initial approximation to the root,
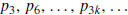, and the terms generated by Aitken’s acceleration method (4).
The second and third columns of Q contain the terms generated by Newton’s method.
The stopping criteria in the program are based on the difference between consecutive
terms from the first column of Q.

Numerical Methods Using Matlab, 4^th Edition, 2004