The Major Topics of School Algebra
Without any knowledge of the historical background of the
logarithm, many students
have come to regard it as another function they need to learn to pass an exam,
with no
appreciation whatsoever of the almost magical property that log x changes
multiplication
to addition.
Fixing a base a, a > 0 and a ≠ 1. Then the functions
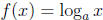and g(x) = ax are
inverse functions, the domain of f being all positive numbers. Thus
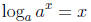for all x
and
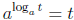for all positive t
These two relations , which characterize the fact that
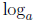and ax are inverse functions, are
the key to solving equations of the following type: find x so that
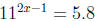. Equations
of this type come up in applications, because nature seems to dictate that
natural growth
and decay processes be modeled by exponential functions, more specifically, by ex
and
variants thereof. There is potential for real excitement here as simple carbon
dating
problems can be discussed in this context.
Problems about changing bases in logarithms are good for testing students’ basic
understanding
of the definitions, but should not be elevated to the status of a major topic.
(Compare the discussion about factoring quadratic polynomials .)
The last collection of functions to receive attention in school algebra are from
outside
algebra: the trigonometric functions. These are functions that are initially
defined only for
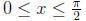(we use radian measure), so the first order
of business is to extend the definition
of sine, cosine to 0 ≤ x ≤ 2π , and then to all values of x by
demanding periodicity of
period 2π , namely, sin(x ± 2π ) = sin x, and the same for cosine.
Thus sine and cosine
become defined on the whole number line . They turn out to be the prototypical
periodic
functions, because in advanced mathematics one shows that any function f which
satisfies
f(x±2π ) = f(x) for all x can be expressed in terms of sine and cosine in a
precise sense .
The restriction to 2π as the period is more apparent than real because, if a
positive
number c is given, then the function h(x) = a sin(2π x/c) is periodic of
period c (i.e.,
h(x±c) = h(x) for all x), and has maximum value |a| and minimum value −|a|.
Students
should have instant recall of the graphs of sine and cosine. In particular, sine
is increasing
in the interval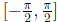 
and therefore has an inverse
function there. Similarly, cosine is
decreasing on [0, π] and it too admits an inverse function there.
One of the reasons that sine and cosine are important in mathematics and science
is
that nature is full of periodic phenomena.
Once sine and cosine are fully understood, the study of
the other four trigonometric
functions becomes fairly routine. Tangent is the most important of these four
and its
graph too should be accessible to instant recall. Note that tangent is not
defined at all
odd integer multiples of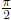 
.
We have mentioned the use of exponential and logarithmic functions to model
growth
and decay and the use of sine and cosine to model periodic phenomena. The use of
linear functions to model certain observable phenomena should also be mentioned
in this
connection. Generically, some observational data, when properly graphed, seem to
suggest
a linear relationship although the data do not appear to be strictly linear due
to inevitable
observational inaccuracies. In such situations, one employs the method of least
squares
to arrive at a linear function that is a “best fit” for the data. The details of
the method are
beyond the level of school mathematics, but the main idea of the method can
nevertheless
be conveyed in a qualitative way. The use of computer software, or even a
programmable
calculator, to produce the “line of best fit” may be used, with guidance, to
advantage to
give an intuitive understanding of this process.
Algebra of Polynomials
Algebra at a more advanced level becomes an abstract study of structure. School
algebra, at some point, should introduce students to such abstract
considerations. The
study of polynomials provides a good transition from algebra as generalized
arithmetic to
abstract algebra. Rather than considering a polynomial as the sum of multiples
of powers
of a number x, we now consider sums of multiples of powers of a symbol X,
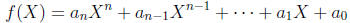
where the 
are constants (i = 0, 1, . . . , n), and
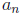≠ 0. To avoid confusion with the
polynomials we have been working with so far, we will call such an f(X) a
polynomial
form, but will continue to refer to n as its degree, the
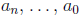as its coefficients, and
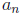as its leading coefficient. The term
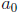will also be referred to as its constant term.
As a matter of convention, we will omit the writing of a term if its coefficient
is 0. Thus
2X2 + 0X + 3 is abbreviated to 2X2 + 3. We define two
polynomial forms to be equal
if their corresponding coefficients are pairwise equal. In particular, two equal
polynomial
forms must have the same degree, because they must have the same leading
coefficient.
Note that the concept of the equality of polynomial forms is a matter of
definition and is
not subject to psychological interpretations. This should help clarify the
current concern
about the meaning of the equal sign in the mathematics education research
literature.
We now single out a special case of the equality of polynomial forms for further
discussion
because it is a delicate point that can lead to confusion. Given a polynomial
form
f(X), what does it mean to say f(X) ≠ 0? In this instance, the “0” can only mean
the
“0 polynomial form”, i.e., “0” here means the polynomial form whose coefficients
are all
equal to 0. Therefore, as polynomial forms, the statement f(X) ≠ 0 means that
the two
polynomial forms f(X) and 0 are not equal. From the preceding definition of the
equality
of polynomial forms, we see that f(X) ≠ 0 means there is at least one
coefficient of
f(X) which is nonzero. Thus X2 − 1 ≠ 0. The reason this may be confusing is
that, if
one is not careful, one might think of X2 − 1 ≠ 0 as the statement that the
polynomial
x2 −1 is never equal to 0 for any number x. Obviously the latter is
not true, e.g., x2 −1
is equal to 0 when x = ±1. In this instance, one has to exercise care in
distinguishing
between a polynomial and a polynomial form.
We do not assume that we have any prior knowledge of the symbol X. The addition
or multiplication of polynomial forms therefore becomes a matter of definition,
i.e., it
is up to us to specify how to do these arithmetic operations among polynomial
forms
because such an f(X) is no longer a number. We do so in the most obvious way
possible,
which is to define addition and multiplication among polynomial forms by
treating X as
if it were a number, so that at least formally, dealing with polynomial forms
does not
introduce any surprises. The idea is so simple that, in place of the most
general definition
possible (which would require the use of symbolic notations not appropriate for
school
mathematics), it suffices to indicate what is intended by a typical example in
each case.
Thus let
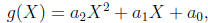and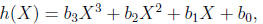 
where the 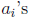and
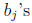are numbers, and
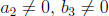. Then by definition,
their sum is
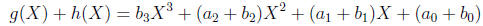
and their product is
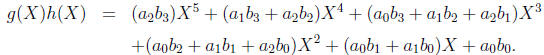
In other words, the product of two polynomial forms is obtained by multiplying
out all
possible terms and then collecting like terms by their powers. It is immediately
seen that,
because the additions and multiplications among the
coefficients are associative, commutative,
and distributive, so are the addition and multiplication of polynomial forms.
Why polynomial forms instead of just polynomials? This question cannot be
answered
satisfactorily in the setting of school mathematics. The idea roughly is that,
since in a
polynomial f(x), the variable x plays the primary role whereas the (constant)
coefficients
play a subordinate role, it is conceptually more clear to disengage x from the
coefficients
altogether. By singling out x as a symbol X in this manner, we open the way for
X to
assume other values distinct from those of the coefficients. For example, in
linear algebra,
one allows X to be a square matrix to obtain the so-called characteristic
polynomial of the
matrix. Moreover, it will be observed that the addition and multiplication of
polynomial
forms depend only on the fact that the coefficients obey the associative,
commutative, and
distributive laws . Anything we say about polynomial forms that depends only on
addition
and multiplication therefore becomes valid not just for real numbers as
coefficients, but
also for any number systems that satisfy these abstract laws, such as the
complex numbers
that will be taken up presently. This is an example of the power of abstraction
and
generality in algebra.
In a limited way, we can illustrate the advantage of the abstraction by
considering the
problem of division among polynomials. Imitating the fact that the division of
polynomial
functions leads to rational functions, we introduce a rational form as any
expression of
the type
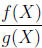, where f(X) and g(X) are polynomial forms, and g(X) ≠ 0.
(Recall that g(X) ≠ 0 merely means that at least one coefficient of g(X) is not
equal to
0.) We also agree to identify every polynomial form f(X) with the rational form
.
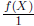For example, 0 is identified with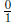 
. We again emphasize that as it stands,
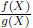is just
a formal expression, and it is up to us to give it meaning. First, what does it
mean that
two such expressions are equal? Given two rational forms
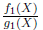and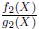 
, we define
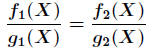
to mean
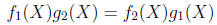
Thus, every rational form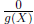 
is equal to 0. In other words, we rely on the crossmultiplication
algorithm in fractions as a guide to define the equality of rational forms.
As a consequence, “equivalent fractions” is automatically
valid among rational forms, in
the sense that for all polynomial forms f(X), g(X), h(X), we have
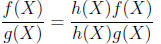
We also define the addition and multiplication of rational forms by imitating
fractions:
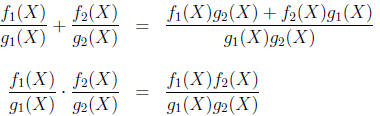
One then shows that these operations are well-defined, and that a rational form
has
the desired property of the division of f(X) by g(X), in the sense that
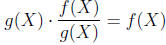
Note also that every nonzero rational form
has a multiplicative inverse
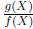. This
completes the analogy that the set of rational forms is to the set of polynomial
forms as
the rational numbers are to the integers.
It may be wise to soft-pedal the well-definedness of the addition and
multiplication of
rational forms in a school classroom and use the time instead on more
substantive things,
such as the division algorithm and its consequences (see below).
If we were constrained to discuss polynomials rather than polynomial forms, then
we
would be faced with the awkward situation regarding the domain of a rational
function
: it is not the number line but the points on the number line outside the
zeros of g(x),
so that the domain of a sum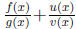
is the set of the point on the number line outside the
zeros of both g(x) and v(x), etc. But for polynomial forms, we have seen from
the above
discussion concerning a polynomial form being nonzero that there is no such
awkwardness.
The analogy of polynomial forms with whole numbers leads us to consider the
analog
of division-with-remainder among whole numbers in the context of polynomial
forms.
This is the important division algorithm for polynomial forms: given any
polynomial
forms f(X) and g(X), there are polynomial forms Q(X) and r(X) so that
f(X) = Q(X)g(X) + r(X)
where r(X) is either 0 or has a degree < the degree of g(X). The reasoning is
essentially
a repackaging of the familiar procedure of long division among polynomials. This
is a
basic fact about polynomial forms in the school algebra curriculum. We note
explicitly
that for the division algorithm to be valid, it is essential that beyond the
associative,
commutative, and distributive laws , the coefficients have the property that a
nonzero
number has a multiplicative inverse.
| Prev | Next |