Quadratic Forms, Critical Points, Principal Axes, and the 2nd Derivative Test
Quadratic Forms , Critical Points, Principal Axes, and the 2nd Derivative Test
A typical question from multivariable calculus is:
Find all critical points of the function
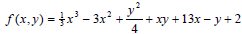 . .Determine which give relative maxima, relative minima, or saddle points. |
As you recall, we first find the critical points for this function. This gives us:
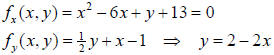
So, we must have x2 - 6x + (2 - 2x) + 13 = x2 - 8x + 15 =
(x - 3)(x - 5) = 0
These yield the two critical points (3,-4) and (5,-8). The next question is
then:
| Do these critical points give maxima, minima, saddle points, or what? |
To answer this question, we generally appeal to the 2nd Derivative Test, which can be formulated as follows:
| Let f (x, y) be a function which is continuous,
with continuous first and second partial derivatives. Define the Hessian matrix to be the (symmetric) matrix consisting of the 2nd partial derivatives, i.e. 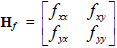 . Let . Let
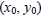 be a critical point for this function. be a critical point for this function.If 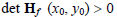 , then , then
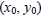 will give a relative maximum or
minimum for this function. will give a relative maximum or
minimum for this function.If either 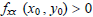 or or
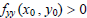 , then there is a
relative minimum at , then there is a
relative minimum at 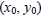 . .If either 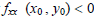 or or
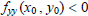 , then there is a
relative maximum at , then there is a
relative maximum at 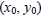 . .If 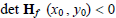 , then , then
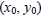 will give a saddle point for
this function. will give a saddle point for
this function.If 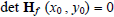 , then there is insufficient information
provided by the 2nd derivatives to , then there is insufficient information
provided by the 2nd derivatives todistinguish between a possible relative maximum, relative minimum, or saddle point at 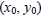 for forthis function. That is, the 2nd derivative test is inconclusive. |
The 2nd Derivative Test is derived from the idea of
quadratic approximation. It is easily shown that the quadratic function
that best approximates a given (sufficiently differentiable) function f (x, y)
in the vicinity of a point 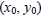 is given by:
is given by:
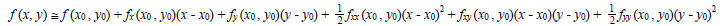
If we denote by 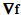 the (gradient) row vector
the (gradient) row vector
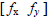 , and let
, and let 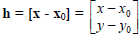 , and if we further write x = (x, y) and
, and if we further write x = (x, y) and
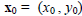 , then the above expression becomes :
, then the above expression becomes :
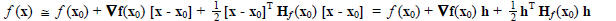 (Verify this!)
(Verify this!)
At a critical point 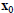 the situation is much simpler, since
the situation is much simpler, since
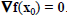 . In this
case, the quadratic approximation is simply:
. In this
case, the quadratic approximation is simply:
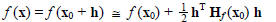 where h is small
where h is small
Thus, the question of whether there is a maximum, minimum, saddle point, or
whatever at 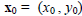 boils down to our
boils down to our
being able to understand the quadratic form  , and, in particular,
what its sign is for any h.
, and, in particular,
what its sign is for any h.
Definition: A quadratic form in Rn is a function q(h) of the form
q(h) = hTAh
for some symmetric matrix A. In other
words, a quadratic form is just a 2nd degree expression involving the
coordinates 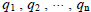 .
.
Example: The quadratic function q(x, y, z) = x2 + 3y2 -
2z2 + 7xy - 6yz is a quadratic form. Note that it has neither a
constant term nor any linear terms . You may verify that with
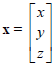 and
and 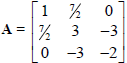 , we have
q(x) = xTAx.
, we have
q(x) = xTAx.
Definition:
A quadratic form q(h) (and its matrix A) is called positive definite
if q(h) > 0 for all h ≠ 0.
A quadratic form q(h) is called negative definite if q(h) < 0 for all
h ≠ 0.
A quadratic form q(h) is called positive semi-definite if q(h)
≥ 0 for all h ≠
0.
A quadratic form q(h) is called negative semi-definite if q(h)
≤ 0 for all h ≠
0.
A quadratic form q(h) is called indefinite if q(h) takes on both positive and
negative values.
The most important fact that we’ll need is the:
| Spectral Theorem: A square matrix A can be diagonalized via an orthonormal change of basis if and only if the
matrix A is symmetric. In particular, all of the eigenvalues of a symmetric matrix are real and an orthonormal basis of eigenvectors may be found. These basis vectors are called the principal axes for the matrix. |
Given a quadratic form q(h) = hTAh, with A symmetric,
there is a orthonormal basis
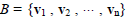 of eigenvectors
of eigenvectors
of A, an orthogonal matrix P whose columns are the vectors of B, and
P-1AP = PTAP = D, a diagonal matrix whose
diagonal entries are the (real) eigenvalues of A. Thus A = PDPT and, if we
define 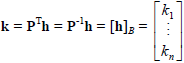 we have:
we have:
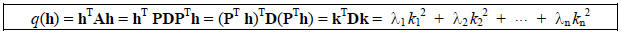
In this form, it is easy to see that:
A quadratic form q(h) is positive definite if all eigenvalues of A are strictly
positive.
A quadratic form q(h) is negative definite if all eigenvalues of A are strictly
negative.
A quadratic form q(h) is positive semi-definite if all eigenvalues of A are
either positive or zero.
A quadratic form q(h) is negative semi-definite if all eigenvalues of A are
either negative or zero.
A quadratic form q(h) is indefinite if some of the eigenvalues of A are positive
and some are negative.
From this, we conclude:
| 2nd Derivative Test (second form): A critical
point for a function f (x) will give: (1) a relative minimum if all eigenvalues of the Hessian matrix 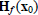 are strictly positive.
are strictly positive.(2) a relative maximum if all eigenvalues of the Hessian matrix 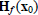 are strictly negative.
are strictly negative.(3) neither a relative maximum nor a relative minimum if some of the eigenvalues of 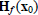 are positive and some are positive and someare negative. (4) Further analysis is necessary in the case where the Hessian matrix 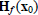 is positive semi-definite (a relative is positive semi-definite (a relativeminimum or neither) or negative semi-definite (a relative maximum or neither). |
The reasoning behind (4) is simply that the second
derivative test is based on a quadratic approximation and in the
borderline case where an eigenvalue is zero , we cannot rely on this
approximation to make any valid conclusions.
Notice that for a function of two variables , in cases (1) and (2) the
determinant of the Hessian matrix will be the product of
the two eigenvalues and will be positive. In the case where both eigenvalues are
positive, the trace of the Hessian matrix
(the sum of its diagonal terms = the sum of its eigenvalues) will be positive
and hence either 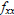 or
or
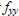 must be positive. In
must be positive. In
the case where both eigenvalues are negative, the trace of the Hessian will be
negative and hence either 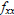 or
or
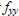 must be
must be
negative. In case (3) for a function of two variables, the determinant will thus
be negative. In case (4), the determinant will
be zero. These observations yield our earlier version of the 2nd derivative
test.
This second version of the second derivative test actually
tells us quite a bit more. It tells us that there is a new coordinate
system defined in the vicinity of a given critical point, based on the principal
axes, in which
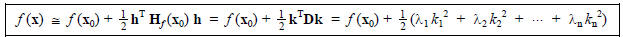
This tells us, in particular, that, in the vicinity of
this critical point, changes in the function will be most sensitive to
changes in the direction of the eigenvector associated with the eigenvalue of
largest magnitude.
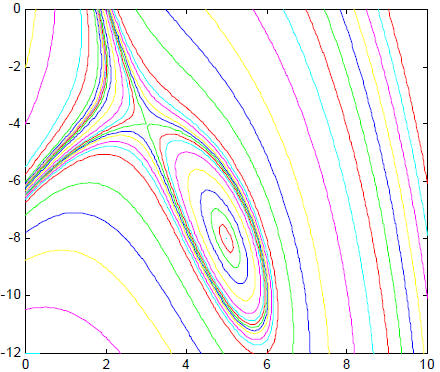
In conclusion, here’s an unlabeled contour diagram for the function
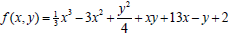 with
with
its two critical points, a saddle point at (3, -4) with f (3, -4) = 19, and a
relative minimum at (5, -8) with 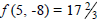 .
.
You may want to carry out the calculations above at each of the critical points
to find the associated eigenvalues and
principal axes and relate what you find to the shape of the contours in the
vicinity of the relative minimum at (5, -8) and, in
particular, which directions give maximum growth.
Exercises: For each of the following functions, find all
critical points and determine, for each critical point, whether it
gives a relative maximum, a relative minimum, or neither. Use eigenvalue
analysis to justify your answers. At any
minimum, determine which directions (from the critical point) will produce the
fastest incremental increase in the
function’s values per distance. At any maximum, determine which directions (from
the critical point) will produce the
fastest incremental decrease in the function’s values per distance.
(Note: Despite the seemingly complicated algebra , you should be able to find all
the critical points. Really, I swear.)
#1: f (x, y) = x3 + 22x2 + 41y2 - 24xy - 176x - 68y + 500
#2: f (x, y, z) = 4x3 - 4y3 -26x2 + 21y2 - 3z2 - 2yz + 56x -30y + 22z
| Prev | Next |