Get it on Google Play Get it on Apple Store

Linear Equations and Regular Matrices

Theorem 5 Let A be a square matrix. Then the column vectors of A are
linearly independent if and only if det(A) ≠ 0.

A square matrix A with det(A) ≠ 0 is called regular; a square matrix A
with det(A) = 0 is called singular.

When the number n of rows and columns of A is large, the formula for
computing det(A) is quite complicated, and calculating det(A) is best left to
the computer. You will only be responsible for computing det(A) by hand
only if A has dimensions 2 × 2, that is, if

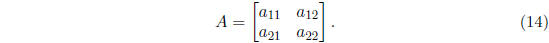
In this case the formula for the determinant becomes:

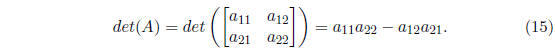
Exercise 6 Consider the matrices

(a) Find det(M) and det(N).
(b) Use the result of (a) to determine whether the column vectors of M are
linearly independent ; similarly for the column vectors of N.
(c) Try to derive the results you obtained in point (b) directly from the
definition of linear independence.

Now let A be a square matrix. An inverse matrix of a square matrix A
is a matrix A-1 such that A-1A = I. Recall that the identity matrix I acts
with respect to matrix multiplication like the number 1 for multiplication
of numbers, that is, BI = B = IB whenever these products are defined .
Thus A-1 can be thought of as a kind of reciprocal of a matrix A. This
analogy can be spun a little further: Not every real number has a reciprocal
(0 being the exception here) and similarly, not every square matrix has an
inverse. However, if A-1 exists, then A-1 is uniquely defined (thus we can
speak about the inverse matrix of A), and we also have AA-1 = I. A square
matrix that has an inverse matrix A-1 is called invertible.

Finding inverse matrices requires quite extensive computations and we
will leave these to the computer. However, if we want to verify that a given
matrix B is the inverse matrix of a given square matrix A, all we need to
do is to compute the matrix product BA (or AB) and check whether the
product evaluates to I.

Exercise 7 Let

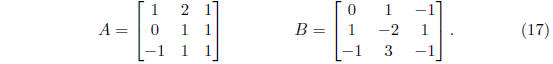
Verify that B is the inverse matrix of A.

Now let us look at the system (1) in yet another way. Let

Exercise 8 By writing out the definition of matrix multiplication, convince
yourself that 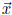is a solution of system (1) if and only if

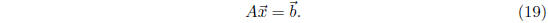
Equation (19) is called the matrix version of system (1); it says the same
as (1), only in matrix notation. Note that Equation (19) looks very similar
to the linear equation

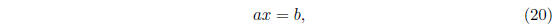
where a; b are given real numbers and x is an unknown real number. If
a ≠ 0, we can solve Equation (20) by multiplying both sides of it by a-1
and we get:

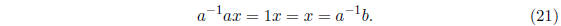
Now suppose A is an invertible square matrix. Let us multiply both
sides of (19) from the right by A-1. We get:

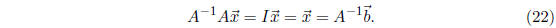
Thus as long as the coefficient matrix of (19) is an invertble square
matrix, we can solve the system by multiplying the right-hand side of (19)
by the inverse of the coefficient matrix.

Exercise 9 Show that the inverse matrix of the coefficient matrix of the
system (4) of Exercise 2 is given by

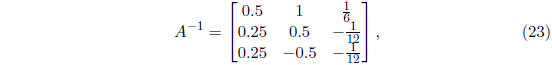
and use this fact to solve system (4).

You will have noticed that the solution of (4) that you found in Exercise 9
is unique. It has to be unique if A has an inverse matrix, since both the
inverse matrix and the product of matrix multiplication on the right-hand
side of (22) are uniquely determined. Thus we have noticed an important
connection: If the coefficient matrix A of (1) is invertible, then (1) has a
unique solution. It can be shown that this also works the other way around:
If a linear system (1) with a square coefficient matrix A has a unique solution,
then this coefficient matrix A must be invertible.

So, when, exactly, is a square matrix invertible? Let us take a square
matrix A and consider the homogeneous system

As we just saw, A is invertible if and only if (24) has a unique solution. As
you showed in Exercise 1, the zero vector 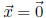is always a solution of (24),
and we found earlier in this note that 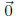is the unique solution of (24) if and
only if the column vectors of A are linearly independent. By Theorem 5 in
turn, this is the case if and only if det(A) ≠ 0. Thus a square matrix is
invertible if and only if it is regular.

We have considered a lot of properties of square matrices in this note.
These properties are stated in different terminology , but in the end, they
all say the same thing about the matrix. Mathematicians refer to this kind
of situation by saying that the properties are equivalent. Let us summarize
what we have learned in a single theorem:

Theorem 10 Let A be a square matrix. Then the following conditions are
equivalent:

1. A-1 exists, that is, A is invertible.

2. The column vectors of A are linearly independent.

3. det(A) ≠ 0, that is A is regular.

4. Every system 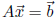has a unique solution.

5. The zero vector is the unique solution of the homogeneous system


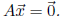
For convenience and completeness, let us also state a version of Theo-
rem 10 for noninvertible matrices:

Theorem 11 Let A be a square matrix. Then the following conditions are
equivalent:

1. A-1 does not exist, that is, A is not invertible.

2. The column vectors of A are linearly independent.

3. det(A) = 0, that is, A is singular.

4. Every system 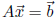is either inconsistent or underdetermined.
5. The homogeneous system 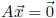has a nonzero solution .

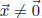Prev Next