Miscellaneous Math Topics
2 Logarithms/Exponents
2.1 Exponents
Exponents are the superscripts on numbers or other mathematical operations.
Exponentiation is sometimes called raising a number to a power. This process
involves two numbers : the exponent and the base. The result is a power of the
base. For example, in the argument an = x, a is the base, n is the
exponent,
and x is the nth power of a. This is equivalent to raising a to the nth
power.
For example:
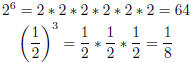
Any number raised to the 1st power is itself
and any number raised to the 0th
power is one . For example:
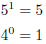
Complex arguments can also be exponentiated and exponents
may themselves
be complex arguments. For example:
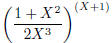
The polynomial quotient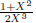 
is raised to the (X + 1)th power. Raising a
nonzero number to the -1 power is to take the inverse of the number, or in other
words, to produce the number’ s reciprocal . For example:
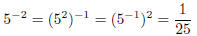
Note that in this example I factor the components of -2
into -1 and 2 to make
the steps clearer . This is one of the allowable operations on integers:
• Multiplying exponentiated numbers with the same base is done by adding
the exponents: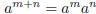 
. For example:
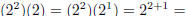
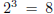. This also works with negative exponents :
. For
example: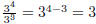
. Equivalently ,
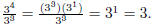
• Exponentiating an exponentiated number is done by multiplying the ex-
ponents: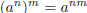 
. For example,
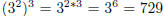. To check
this, note that 
.
• Exponents can be factored: 
.
This can be useful: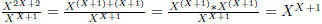 
• Numbers with the same base and same exponent can be added :
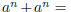
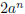and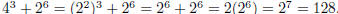 
Exponential functions are often used to model growth and decay because
they multiply at a constant rate. For example, a population that doubled in
size every 25 years could be modeled with an exponential function.
Exercises: Exponents
1. Simplify (x2 + 3x) + (2x2 + 2x +
5)
2. (2x2)(x2)
3. Calculate (32)2
4. Calculate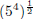 
2.2 Logarithms
Like the exponent , the logarithm involves two numbers, the base number and
the number that the logarithm acts on. Logarithm is the inverse operation of
exponentiation (they “undo” eachother). The logarithm of a number x in base
b is the number n such that x = bn. Here is the notation:
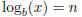
This is read “log base b of x equals n.” By definition, if
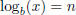, then x = bn.
For example:
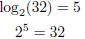
Consider the equation b x = n. If we know b and
x, we calculate n where n is a
power of b. If we know x and n, we find b by taking the xth root (or
radical) of
n. If we know b and n, we compute a logarithm to find x. For example:
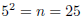
b3 = 27 becomes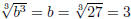 
so b = 3
4x = 4096 becomes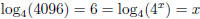 
so x = 6
The allowable operations on logarithms are:
• The product rule :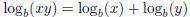 
• The quotient rule: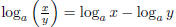 
• The power rule: 
Using these rules and the definition of the logarithm, we can see how the
logarithm is the inverse of the exponential: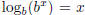 
and 
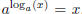. To
better understand the inverse relationship between logarithm and exponentia-
tion, consider these equations more closely:
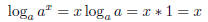
The product rule allows me to rewrite
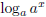as 
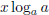. By
definition,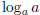 
produces a number n such that an = a; clearly, n=1. Therefore,
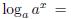
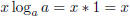. Now, consider the other equation:
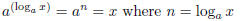
By definition,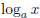 
produces the number n such that an = x. Therefore,
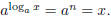
Exercises: Logarithms
1. Calculate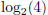 
2.
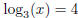.Find x.
2.3 The number e and the Natural Logarithm (ln)
The exponential function is a function of base e raised to some power. The
number e ≈ 2.718 is often used to model growth and decay. It is so
important
that it has its own notation:
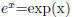
When the base of an exponential function is not e, it is
possible to change the
base :
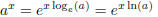
This also works for other base-changes.
Logarithms of base e are “natural logarithms.” They also have their own
notation:
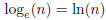
Logarithms of base 10 are also commonly used. When the
base is not specified
(log(n)), it can generally be assumed that it is base 10.
| Prev | Next |