Rational Equations and Inequalities
■Section 3.6
■ Rational Functions are useful models for
■Inverse variation relationships
■Proportion or ratio problems
■Relationships approaching limits
Model: Product Exchange
| Gas | Oil |
| 0 | 100 |
| 10 | 37.69 |
| 20 | 22.86 |
| 30 | 16.21 |
| 40 | 12.43 |
| 50 | 10 |
| 60 | 8.30 |
| 70 | 7.05 |
| 80 | 6.09 |
| 90 | 5.32 |
| 100 | 4.71 |
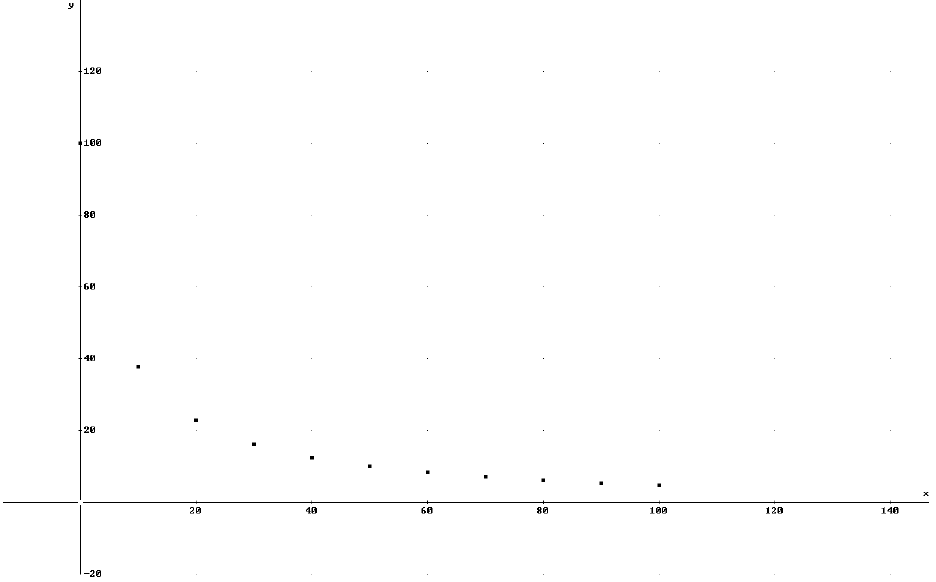
■Product exchange functions give the relationship between quantities of two
items that can be produced by the same factory. An oil refinery can produce
gasoline, heating oil, or a combination of the two . Data was collected for gas
versus heating oil production in 1000 gallon allotments
■Determine a model for the product-exchange of gas and heating oil.
■View the graph in the next slide and address these questions
■What functions have we studied that have the same concavity and decreasing
trend as the data?
■What in the context of the problem indicates choosing one of these functions
over the other?
Product Exchange
Rational Function Model
■Serves as good model for data that approaches a fixed value or a limiting
value since rational functions have asymptotes.
■Serves as a good model when the context is a ratio or comparison , such as gas versus heating oil
■How do we determine a rational model?
■Derive 5and Graphing calculators do not
fit rational functions to data
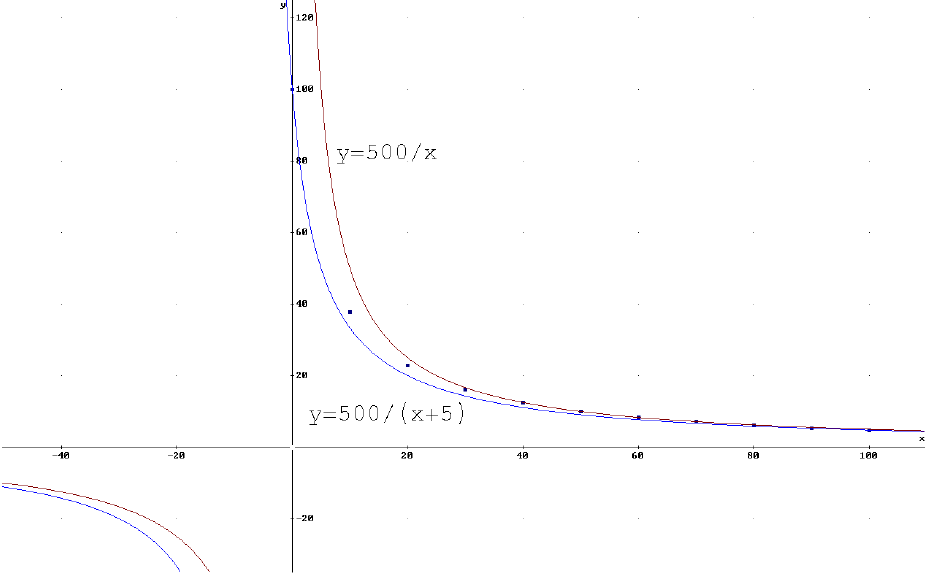
■Estimate model using basic rational power
function y = A/x. Will A > 1 or A < 1?
■Solution: Using graphing technology and
eyeballing the curve of best fit we get
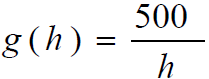
■Translate to start at
(0,100)
Power Function Models
Actual Model
■Difficult to find actual model
■ Linearize the data (using Exercise 51 or 53)
■Determine from other problem context not provided
■Solution:
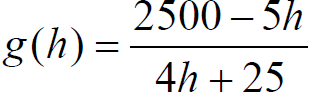
Rational Equations
■Determine the heating oil production if the gas production is 15 of the 1,000
gallon allotments.
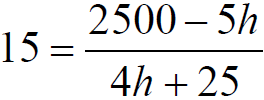
■How do we solve rational equations?
Solving Rational Equations
■ Convert the rational equation into a polynomial equation by multiplying by the least common denominator
■Solve the resulting polynomial equation
■Check the solutions to be sure none of them are extraneous
■Use graphic methods if analytic methods fail
■Solve the following example
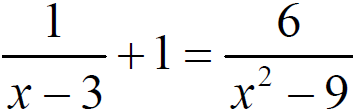
■Class Participation Activity
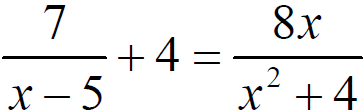
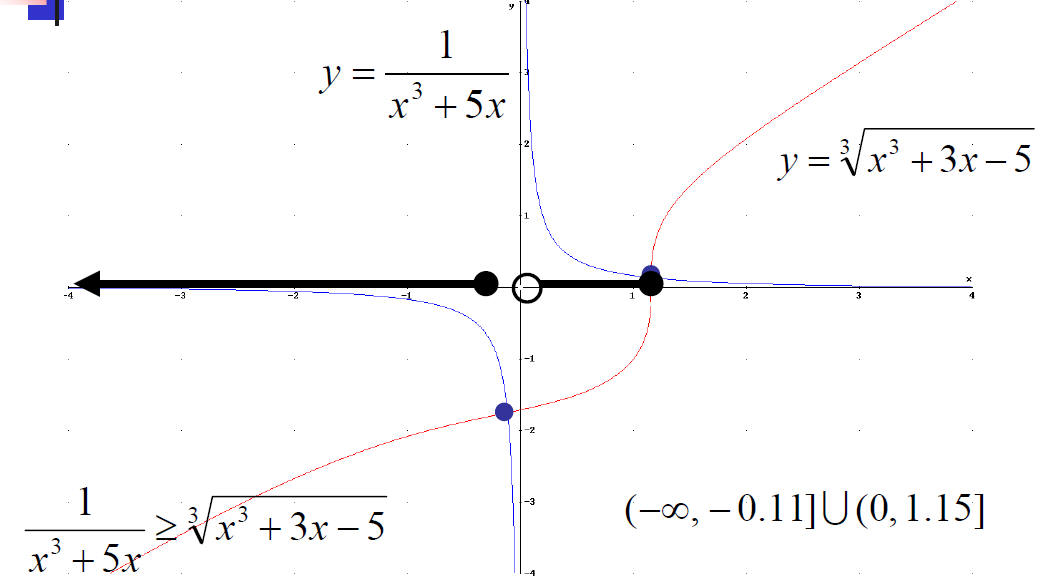
Solving Inequalities
■Solve inequalities with higher degree polynomial, radical, absolute value,
or rational expressions using the graphic method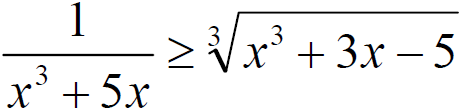
■Either set to zero and write one related function
■Or write a related equation for each side of the
inequality
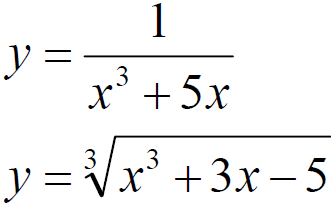
Solving Inequalities –
Graphic Method
Transformation of
Algebraic Functions
■Given any algebraic function y = f(x) we can transform it.
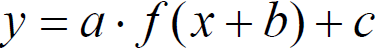
■a > 1 stretch, 0 <
a < 1 compress, a < 0 reflection in x-axis
■b > 0 translation left, b < 0
translation right
■c > 0 translation up, c < 0 translation down
■Try translating
the following function
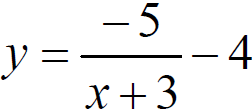
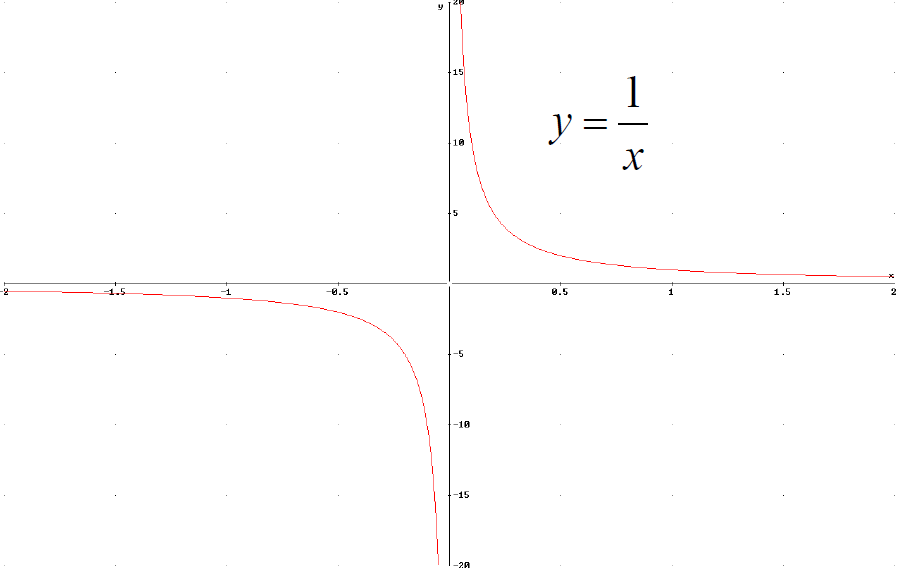
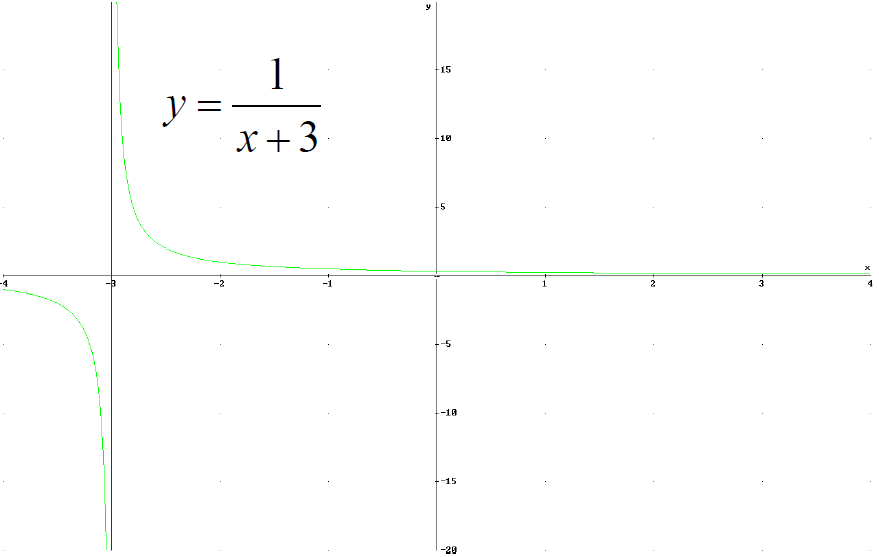
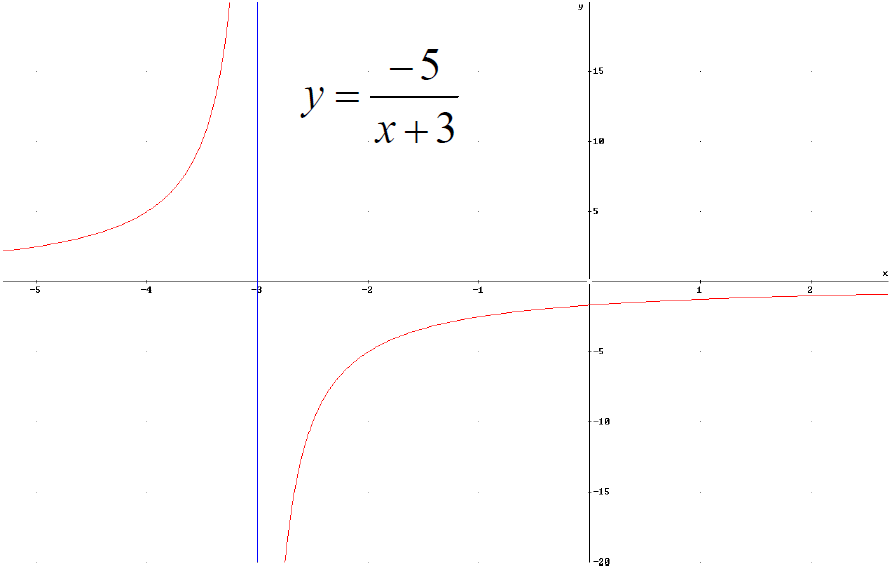
| Prev | Next |