Proficiency Algebra Review Sheet
1 Introduction.
This is a review sheet for MAP 103: Proficiency Algebra which I will
continue to develop
throughout the semester. You can skip the first section, especially if you're
studying for a midterm
at the last minute, but it is informative, so do read it if you get a chance. If
you get stuck going
from one step to the next in an argument, don't give up, but rather try to
figure out what has
changed from the old step to the new. Usually there will only be one
possibility.
2 Properties of the Real Numbers.
The real numbers are a field, which means that they are endowed with operations
+ and · such
that for any real numbers a, b, c,
1) Associativity of Addition and Multiplication . (a + b) + c = a + (b + c) and (ab)c
= a(bc)
2) Commutativity of Addition. a + b = b + a and ab = ba
3) Existence of Zero and One . ...there are numbers 0 and 1 such that a + 0 = 0 +
a = a and
a1 = 1a = a
4) Existence of Additive and Multiplicative Inverses . For every number a there
is a number -a
such that a + (-a) = (-a) + a = 0. For every number a ≠ 0 there is a number a-1
such that
aa-1 = a-1a = 1.
5) Distributivity of Multiplication Over Addition. a(b+c)=ab+ac
The real numbers are ordered, which means that the exists a relation ≤ such that,
for any real
numbers a, b, c,
6) a ≤ b or b ≤ a
7) a ≤ b and b ≤ a together imply a = b
8) a ≤ b implies that a + c ≤ b + c
9) 0 ≤ a and 0 ≤ b together imply that 0 ≤ ab
These are all properties that are important to know. There is a last property
which, together with
the others, characterizes the real numbers, but you do not need to know it
unless maybe you major
in math. That property is,
Completeness. Let S be a collection of real numbers contained in some interval
(-∞, b]. Then we
can choose a smallest number b' for which S is contained in (-∞, b'].
Why are these properties important? Well, we can use it to define the absolute
value function :
lxl = x if 0 ≤ x. lxl = -x if x ≤ 0.
This function is defined for any real number x by property (6), since we have x≤ 0
or 0 ≤ x. It
just amounts to taking the positive part (or keeping it zero). So l1l = 1 and l
- 2l = 2 and l0l = 0.
We can also use these properties to prove that the square of a real number can' t
be negative .
Suppose x2 ≤ 0. By property (6) we have 0 ≤ x or x ≤ 0. If 0 ≤ x, then by proprety (9),
0 ≤ x2,
so by property (7) x2 = 0.
On the other hand, if x ≤ 0, then by property (8) x-x ≤ 0-x, so that 0 ≤ -x. Then by
property
(7) 0 ≤ (-x)2. So 0 ≤ x2. And again by property (7) x2 = 0.
So the square of a real number can't be negative.
3 Polynomials.
A polynomial is a function of the form
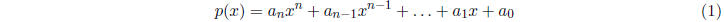
where the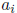 
are real numbers, and n is a nonnegative
whole number. So the following are polyno-
mials:
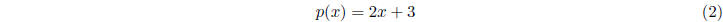
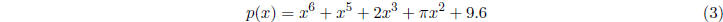
but NOT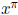 
or
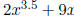or xx or
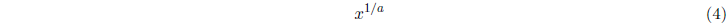
which equals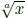 
or
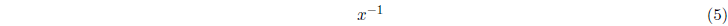
which equals 1/x. Sometimes things that are polynomials
may not look like polynomials. For
example,
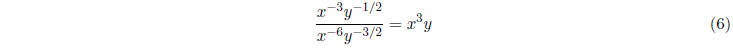
is a polynomial-in both x and y.
The highest exponent n is called the degree or order of
the polynomial. We will mainly concern
ourselves with first and second degree polynomials. To add polynomials, simply
combine like terms
as the following example illustrates:
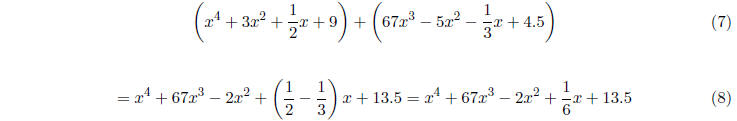
The difference of two polynomials is also a polynomial.
Remember that when you subtract any
kind of sum, you have to distribute the minus sign , since you are really
multiplying by minus one:
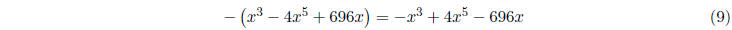
The product of polynomials is also a polynomial. To
multiply polynomials, you have to use the
distributive property. Here is an example:
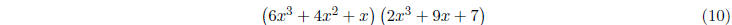
I will rewrite this with brackets. The brackets should
help you follow where everything gets multi-
plied out to:
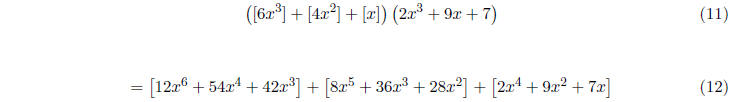
(...now combine like terms...)
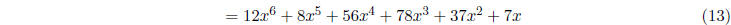
4 Where Does a Polynomial Equal Zero?
Let p(x) be a polynomial. If we plug in a number r and p(r) = 0, then we say r
is a root of that
polynomial . For example,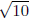
is a root of the
polynomial
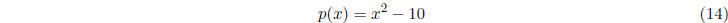
This is (probably) where the term square root comes from.
A second-degree polynomial such as
the one above is called a quadratic polynomial. The most general form of a
quadratic polynomial is
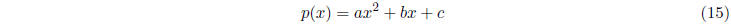
The quadratic formula gives us a formula for the roots of
this polynomial, which exist if and only
if b2 - 4ac ≥ 0. The formula is
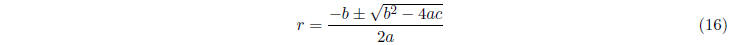
Memorize this. Here is a proof that the formula works
which you don't need to know for the exam,
but is good FYI. If you learn this proof, you will learn something that only a
small percentage of
people on this earth know.
Let ax2 + bx + c = 0. First, we apply a trick called completing the square. Since
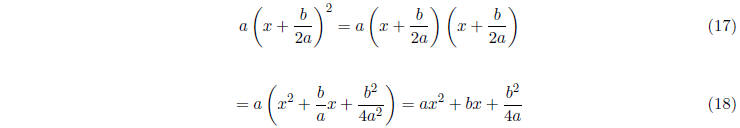
we have
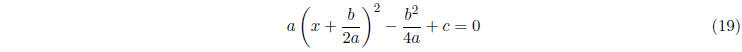
Now let us solve for x:
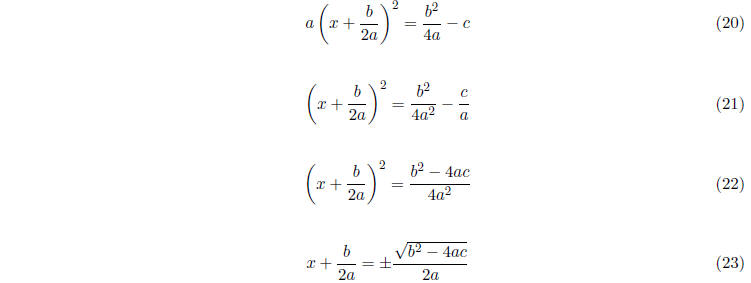
Finally,
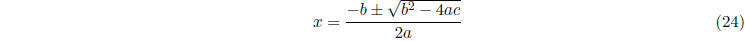
5 Dividing One Polynomial By Another.
If you make a fraction with a polynomial on the top (numerator) and one on the
bottom (denom-
inator), then the result will not always be a polynomial. We call a fraction of
two polynomials a
rational function . Unlike a polynomial, a rational function might not be defined
everywhere. A
rational function is undefined precisely where the denominator equals zero. For
example,
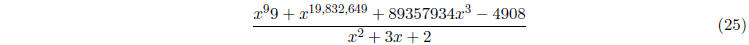
is undefined precisely when x2 + 3x + 2 = 0, in other words
at x = -1 and x = -2.
If you have an equation involving rational functions, you can cross-multiply to
get an equation
involving polynomials. For example, let's try to solve
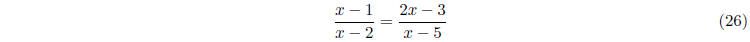
Multiplying both sides by (x - 2)(x - 5) gives us
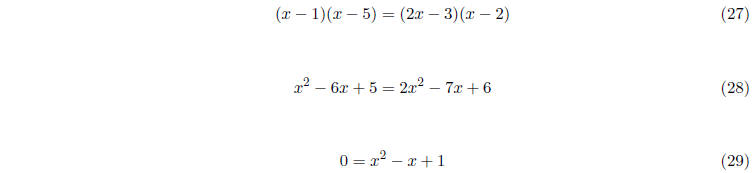
This doesn't have any solutions, because (-1)2 - 4 < 0.
Remember that to add two rational functions together, you just have to make a
common denomi-
nator. So
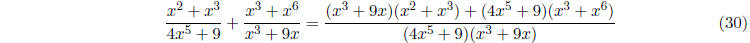
Finally, suppose that a(x)/b(x) is a rational function. Then we can write
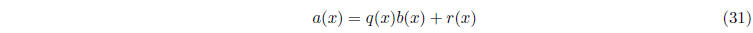
where q(x) and r(x) are polynomials. We call q(x) the
quotient, and r(x) the remainder of the long
division. (We call a(x) the dividend and b(x) the divisor.) Effectively, what we
are doing is long
division of polynomials. I will go over the long division in class before
Midterm 1, so we can get a
proper review on it. It's too unwieldy to type up. Maybe I'll scan a handwritten
example later.
| Prev | Next |