Finding Zeros of Polynomials
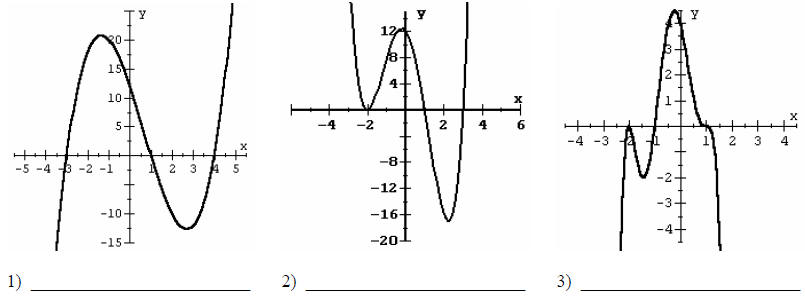
Give a possible factorization of the following polynomials. Do NOT multiply out the factors!
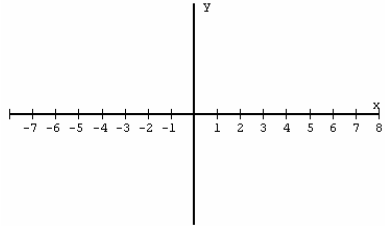
4) Sketch a Graph of a polynomial with the given zeros and corresponding
multiplicities.
(note: the graph is not unique )
x = -5, of multiplicity 2
x = -1, of multiplicity 1
x = 2, of multiplicity 3
x = 4, of multiplicity 2
5) Find the zeros of the following polyno mial function and state the multiplicity of each zero.
f (x) = x (x - 1)2 (2x + 1) (x + 4)3
6) Find a polynomial function of degree 3 with the given
zeros.
Write your answer in the form: f (x) = ax3 + bx2 + cx + d
x = -2 , x = - 1 , x = 2
7) Find a polynomial function ( factored form ) of degree 3
which has the corresponding table of values to the right .
| x | y |
| 4 3 2 1 0 -1 -2 -3 -4 |
18 0 -4 0 6 8 0 -24 -70 |
Factor the following polynomial functions
completely.
Exact answers only!!! No Decimal approximations allowed!
8) FACTOR : f (x) = x5 + 2x4 - 18x3 - 4x2 + 49x - 30
9) FACTOR : f (x) = 6x4 - 7x3 - 73x2 + 14x + 24
List the real zeros of the following polynomial. Exact answers only!!! No Decimal approx.
10) f (x) = x4 + 2x3 - 10x2 - 14x + 21
| Prev | Next |