Factoring

Graphing Rational Functions

1.1 Factoring
The first step in graphing a rational function is factoring polynomials. The
following is an algorithm which will generate all the factors of the form ax+b
where a and b are integers. All other real factors will require the quadratic
formula . The algorithm is described as follows for the polynomial p(x):

• List all factors of the leading coefficient and the constant term.
• Generate a list of all possible factors ax+b where a divides the leading
coefficient and b divides the constant term.
• Test to see if each of these is a factor by plugging -b=a into p. If the
result is 0, you have found a factor.
• Do long division (or synthetic division if appropriate and you prefer)
to determine the other factor.
• Narrow your list of possible factors based on the new polynomial.
• Start over at step 3. Note that a factor may appear more than once.

All Factors of a Number
To find all factors of a number, test all numbers between 1 and the square
root of the number . If one of these divides evenly into the number, then you
have found two factors . As an example, consider the number 60, we will need
to test the numbers from 1 to 7 since 8² > 60.
 

2 divides 60 with quotient of 30
3 divides 60 with quotient of 20
4 divides 60 with quotient of 15
5 divides 60 with quotient of 12
6 divides 60 with quotient of 10
7 does not divide 60

So 60has the factors:
1; 2; 3; 4; 5; 6; 10; 12; 15; 20; 30; 60:

All Possible Factors
Now for every factor of the leading coefficient, a, and every factor of the
constant, b, list the factors ax + b and ax - b provided a and b do not have
a common factor . So if the polynomial were
p(x) = 6x⁴ - 29x³ + 30x² + 11x - 6

we use our factor list above and construct the following factors (note that I
cycle through the q's while fixing the p).

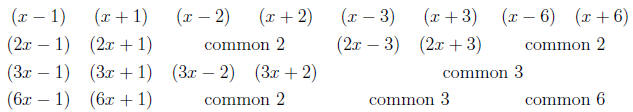
Test Each Factor
The binomial ax + b is a factor of the original polynomial if and only if
p(-b/a) = 0. We work at chipping away at the polynomial until it gets
small enough that we can finish it o . For the polynomial p above:

(x - 1) p(1) = 6 - 29 + 30 + 11 - 6 ≠ 0
(x + 1) p(-1) = 6+29+30 - 11 - 6 ≠  0
(x - 2) p(2) = 6(16)-29(8)+30(4)+11(2)-6 =0
so we do long division and
the quotient will be p₁(x) = 6x³-17x² -4x+3: Note that we can now
eliminate all of the potential factors with constant terms of 2's or 6's.
Thus we can jump to (x - 3).

(x - 3) p₁(3) = 6(27) - 17(9) - 4(3) + 3 = 0 so we do long division and the
quotient will be p₂(x) = 6x² + x - 1. Note that we can now eliminate
all factors with constant terms other than 1. Thus we could jump to
(2x - 1) as the next possible factor. However, in this case, it is easiest
just to "unfoil" it to get (3x - 1)(2x + 1).

The final result is (x - 2)(x - 3)(3x - 1)(2x + 1).

Example
The example is:
x⁵ - 5x⁴ - 9x³ + 41x² + 32x - 60

The factors of 60 are given above and so we check:

(x - 1) p(1) = 1 - 5 -9 + 41+32 - 60 = 0 and so we long divide to get
p₁(x) = x⁴ - 4x³ - 13x² + 28x + 60

(x - 1) p₁(1) = 1 - 4 - 13 + 28 + 60 ≠  0
(x + 1) p₁(-1) = 1 - 4(-1) - 13(1) + 28(-1) + 60 ≠  0
(x - 2) p₁(2) = (16) - 4(8) - 13(4) + 28(2) + 60 ≠  0

(x + 2) p₁(-2) = (16) - 4(-8) -13(4) + 28(-2) + 60 = 0 so we long divide to
get p₂(x) = x³ - 6x² - x + 30

(x + 2) p₂(-2) = (-8)-6(4)-(-2)+30 = 0 so we long divide to get p₃(x) =
x² - 8x + 15 which we can unfoil to (x - 3)(x - 5).

The result is (x - 1)(x + 2)(x + 2)(x - 3)(x - 5).

1.2 Exercises
Factor the following completely over the integers. The final answer should
consist of constants (a), binomials (ax + b) and possibly some quadratics
(ax² + bx + c) which have irrational or imaginary roots.

1. 2x⁴ + 5x³ - 5x - 2
2. 9x⁴ - 24x³ + 22x² - 8x + 1
3. x⁴ + 4x³ + 6x² + 4x + 1
4. x⁴ - 1
5. 10x⁴ + 18x³ - 54x² - 50x + 12
6. 3x³ - 32x² + 83x - 42
7. 11x⁴ - 175x³ + 655x² - 665x - 66
8. 12x⁴ - 16x³ - 53x² - 26x + 15

1.3 Appendix: Descarte's Rule of Signs
We don't have time for this, but someday I will stick it here.
Draft Version: c 1998 Aaron Montgomery