Math 117 Midterm Review 2
First part, free responses.
I. Solve the following problems.
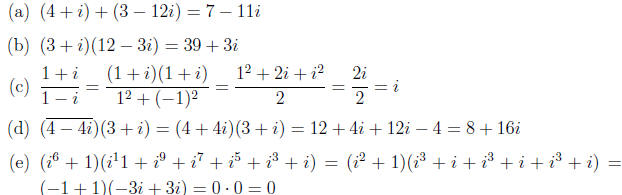
(f) Find the principle square root of −16.
II. Suppose f(x) = (x + 9)(x − 2)2.
(a) Find all x- and y-intercpets.
Setting f(x) = 0, and solving for x, we obtain x-intercepts at points (−9, 0),
(2, 0).
Also in order to obtain y-intercpet, we need to solve f(0). f(0) = (0 +
9)(0 − 2)2 = 36. Therefore y-intercpet is at the point (0, 9).
(b) Determine whether graph touches or crosses x-axis at each x-intercept.
The real zero −9 has a multiplicity of 1, an odd interger, meaning graph
there crosses x-axis.
The real zero 2 has a multiplicity of 2, an even integer, meaning graph there
touches x-axis.
(c) For large value of |x|, the graph will resemble the power function y = x3.
III. Let f(x) = (a − 1)x2 + 4x + 1.
(a) When a−1 < 0, the parabola opens down, so (−∞, 1) should be the answer.
(b) In order for the quadratic function to have two distinct real zeros, the
discriminant need to be positive, i.e., Δ = 42−4·(a−1)·1 = 16−4(a−1) =
20 − 4a > 0. Solving this inequality, we obtain the solution in interval
notation, (−∞, 5).
(c) When a = 5, f(x) = 4x2 + 4x + 1 = (2x + 1)2 ≥ 0, so the
domain for this
quadratic function is (−∞,∞), and the range is [0,∞).
IV. Let f(x) = x2 + 4x − 5.
(a) Completing the squares, we have f(x) = (x2+4x+4−4)−5 = (x+2)2−9.
Hence the vertex should be (−2,−9).
(b) Factoring the polynomial function, f(x) = (x−1)(x+5). So setting f(x) =
0, we obtain the real zeros of f are 1 and −5.
(c) Following part (b), we divide the real number line into 3 sections: (−∞,−5),
(−5, 1) and (1,∞). Setting up a table might clear things up:
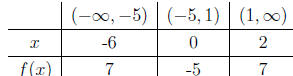
So, in order for f(x) > 0, the solution intervals are
(−∞,−5) ∪ (1,∞).
V. (a) R(p) = p · x = p(−5p + 100) = −5p2 + 100p.
(b) By completing the squares, R(p) = −5(p2 − 20p + 102 − 102) = −5(p −
10)2 + 500. So the vertex is at (10, 500), meaning when price p equals 10,
the quadratic function R(p), revenue, reaches its local maximum of 500.
VI. Suppose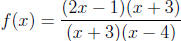 
.
(a) The domain excludes x = −3, 4, so domain of f(x) is (−∞,−3) ∪
(−3, 4) ∪
(4,∞).
(b) Notice that f(x) is not in lowest terms , so we reduce it into
.
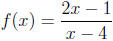Then setting the denominator to 0, we obtain the vertical asymptote x = 4.
(c) We can use long division to obtian the horizontal asymptote, which is y = 2.
VII. Solve inequalities.
(a) x2 − 5x + 4 ≥ 0
x2 −5x+4 = (x−1)(x−4) = 0 → x = 1, 4. So we separate the x-axis into
three parts. Setting up a table:
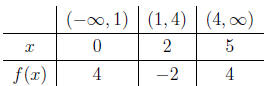
Hence the solution for f(x) > 0 is (−∞, 1) ∪ (4,∞). Also
notice that the
inequality is not strict , we need add solutions for f(x) = 0 into the result,
so we obtain the result as (−∞, 1]∪ [4,∞)
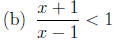
First of all we subtract both sides by 1 and simplify the ineequality , then
we obtain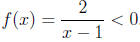 
. So the result is (−∞, 1).
Second part, multiple choices.
1. C.
2. C. By looking at the discriminants.
3. C. Using synthetic division twice, we can obtain the answer.
4. A.
5. E.
6. B.
7. D.
8. B.
9. A.
10. C.
School
| Prev | Next |