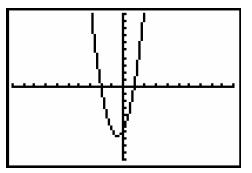
Solving Quadratic Inequalities
EXAMPLE: Solve 3x^2 + 3x – 6 > 0
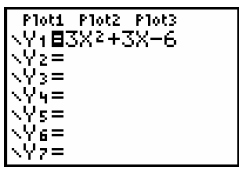
|
Step 1: Press Y= Under Y1 enter the polynomial 3x^2 + 3x – 6 Then press GRAPH We want to find where the polynomial is greater than 0. |
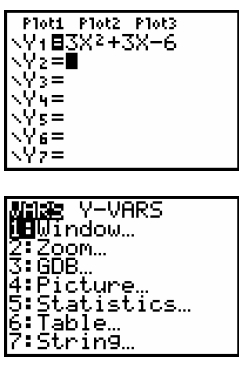 |
Step 2: Go back to Y= We want to know where Y1 > 0, so let’s enter this under Y2 Place the cursor beside Y2= Press the VARS key |
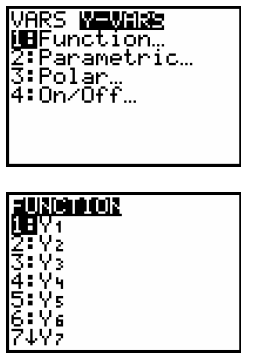 |
Step 3: Arrow over to Y-VARS We want to call up Y1 which is under 1:Function so press ENTER To select Y1 press ENTER again |
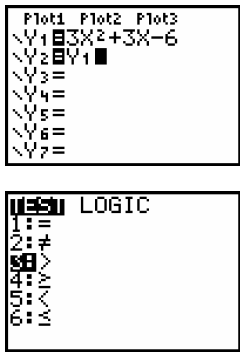 |
Step 4: To insert the inequality symbol , go to the TEST menu by pressing 2nd MATH Arrow down to 3:> and press ENTER |
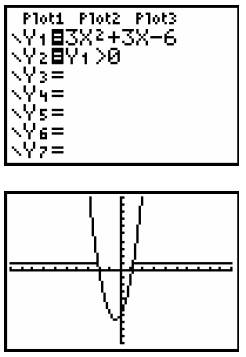 |
Step 5: Now enter 0 and press GRAPH The horizontal lines show which x- values have positive y-values, which is what we are looking for since 3x^2 + 3x – 6 > 0 The x- values are to the left and right of the x-intercepts. |
 |
Step 6: To find the x-intercepts, go to the CALCULATE menu by pressing 2nd TRACE Arrow down to 2: zero and press ENTER |
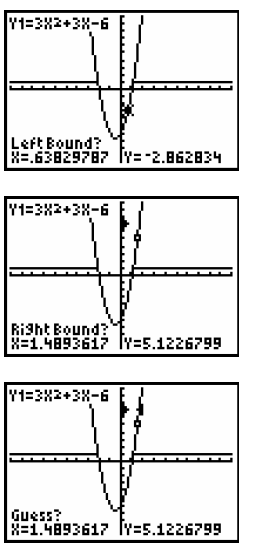 |
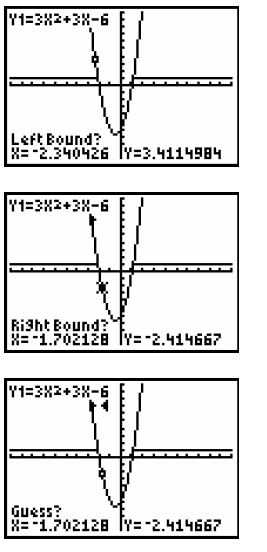
Step 7: To find the intercept on the right , use the arrow keys to move the cursor to the left of the intercept (left bound) and press ENTER Then move the cursor to the right Now press ENTER one more time |
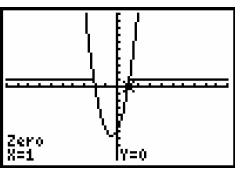 |
The x-value for the intercept is 1 |
 |
Step 8: To find the intercept on the left, we repeat the process. Go to the CALCULATE menu by pressing 2nd TRACE arrow down to 2: zero and press ENTER Use the arrow keys to
move the Then move the cursor to the right Now press ENTER one more time |
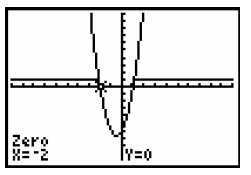 |
The x-value for the intercept is -2 |
So the solution for the inequality is
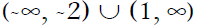
| Prev | Next |