Design of Line Algorithms

Basic Math Review

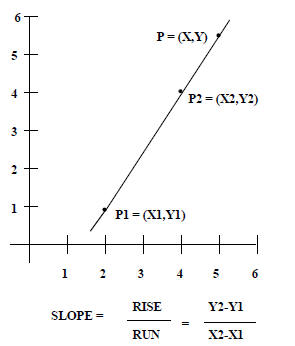
Slope- Intercept Formula For Lines

Given a third point on the line:
P = (X,Y)
Slope = (Y - Y₁)/(X - X₁)
= (Y₂ - Y₁)/(X₂ - X₁)
Solve for Y
Y = [(Y₂-Y₁)/(X₂-X₁)]X
+ [-(Y₂-Y₁)/(X₂-X₁)]X₁ + Y₁
or
Y = mx + b

Length of line segment between P₁ and P₂:
L = ¦ [ (X₂-X₁)² + (Y₂-Y₁)² ]
Midpoint of a line segment between P₁ and P₃:
P₂ = ( (X₁+X₃)/2 , (Y₁+Y₃)/2 )
Two lines are perpendicular iff:
M₁ = -1/M₂

Parametric Form of the Equation
of a 2D Line

Given points P₁ = (X₁, Y₁) and P₂ = (X₂, Y₂)
X = X₁ + t(X₂-X₁)
Y = Y₁ + t(Y₂-Y₁)

When
t = 0 we get (X₁,Y₁)
t = 1 we get (X₂,Y₂)

As 0 < t < 1, we get all points between (X₁,Y₁) and (X₂,Y₂)

Basic Line Algorithm

Must:
1. Compute integer coordinates of pixels which lie on or near a line.
2. Be efficient.
3. Create visually satisfactory images.
• Lines should appear straight
• Lines should terminate accurately
• Lines should have constant density
• Line density should be independent of line length and angle
4. Always be defined.

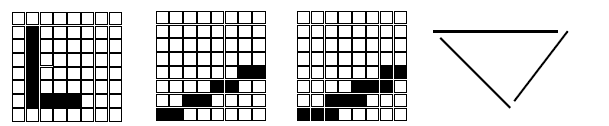
Simple DDA Line Algorithm
{Based on the parametric equation of a line }

Procedure DDA(X1,Y1,X2,Y2 :Integer);
Var Length, I :Integer;
X,Y,Xinc,Yinc : Real ;

Begin
Length := ABS(,X2 - X1);
If ABS(Y2 - Y1) > Length Then
Length := ABS(Y2-Y1);
Xinc := (,X2 - X1)/Length;
Yinc := (Y2 - Y1)/Length;
X := X1;
Y := Y1;

For I := 0 To Length Do
Begin
Plot(Round(X), Round(Y));
X := X + Xinc;
Y := Y + Yinc
End {For}
End; {DDA}

Creates good lines, but problems ...

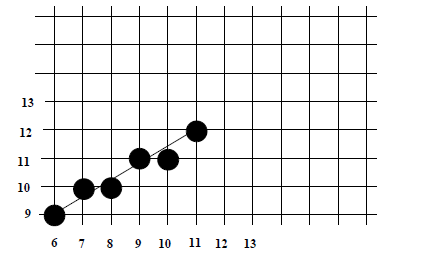
DDA Example

Render the line from (6,9) to (11,12):
Length := Max of (ABS(11-6), ABS(12-9)) = 5
Xinc := 1
Yinc := 0.6

Values computed are:
(6,9),
(7,9.6),
(8,10.2),
(9,10.8),
(10,11.4),
(11,12)

Fast Lines Using The Midpoint Method

Assumptions: line between points (0,0) and (a,b) with

Recall: y = mx + B (m is the slope, B is the y-intercept)
=>m = b/a and B = 0
=>y = (b/a)x + 0
=>f(x,y) = bx - ay = 0

Two choices for next pixel (T or S),
want the pixel closer to line!

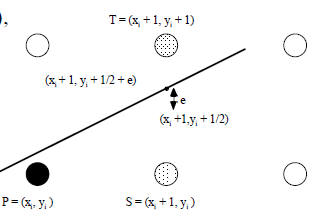
Assume distance between
pixel centers is 1
Midpoint is (x_i + 1,y_i + 1/2)

e is difference between midpoint and where line crosses between
S and T

If e is positive , line crosses above the midpoint and is closer to T
If e is negative , line crosses below the midpoint and is closer to S
=> don’t need exact value of e

Fast Lines - The Decision Variable

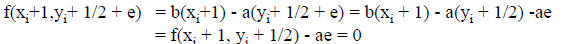
Let 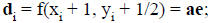d_i is known as the decision variable.
Since a ≥ 0, d_i has the same sign as e.

Algorithm:

If d_i ≥ 0 then
Choose T = (x_i + 1, y_i + 1) as next point

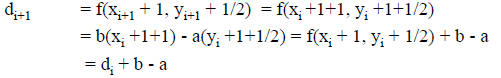
else
Choose S = (x_i + 1, y_i) as next point

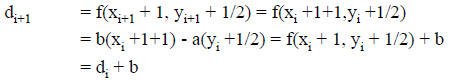
Fast Line Algorithm

Calculate initial value for d₀ directly from f(x,y) at (0,0):
d₀ = f(0 + 1, 0 + 1/2) = b(1) - a(1/2) = b - a/2
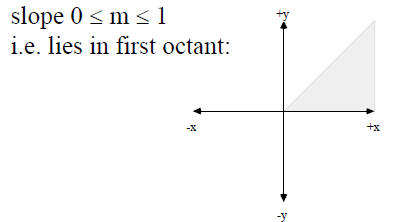
Algorithm for a line from (0,0) to (a,b) in the first octant is:

x := 0;
y := 0;
d := b - a/2;
For i := 0 to a do Begin
Plot(x,y);
If d ≥ 0 Then Begin
x := x + 1;
y := y + 1;
d := d + b - a
End

Else Begin
x := x + 1;
d := d + b
End
End

The only non-integer value is a/2
How can we get rid of it?

Bresenham’s Line Algorithm

Generalize for lines beginning at points other than (0,0)

Begin {Bresenham for lines with slope between 0 and 1}
a := ABS(xend - xstart);
b := ABS(yend - ystart);
d := 2*b - a;
Incr1 := 2*(b-a);
Incr2 := 2*b;
If xstart > xend Then Begin
x := xend;
y := yend
End
Else Begin
x := xstart;
y := ystart
End;

For I := 0 to a Do Begin
Plot(x,y);
x := x + 1;
If d ≥ 0 Then Begin
y := y + 1;
d := d + incr1
End
Else
d := d + incr2
End {For Loop}
End; {Bresenham}

Optimizations

Detect cycles in the decision variable
=>correspond to a repeated pattern of pixel choices
Save pattern, reuse if a cycle is detected

Antialiasing

Aliasing caused by finite addressability of CRT
Approximation of lines with discrete points can result in a
staircase appearance or "Jaggies"

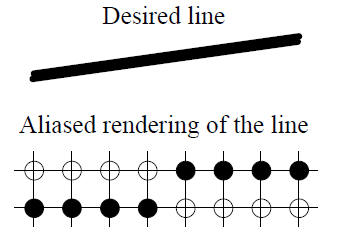
Antialiasing - Solutions

Aliasing can be smoothed out by using higher addressability.
Problem: addressability usually fixed
Solution: intensity is variable, so use it
=> two adjacent pixels can give impression of point part way
between
=> perceived location of point dependent upon ratio of
intensities
An antialiased line has virtual pixels “located” at the proper
addresses

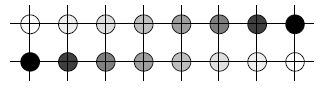
Antialiased Bresenham Lines

Use the distance (e = d_i/a) value to determine pixel intensities.
Three possible cases for the Bresenham algorithm:

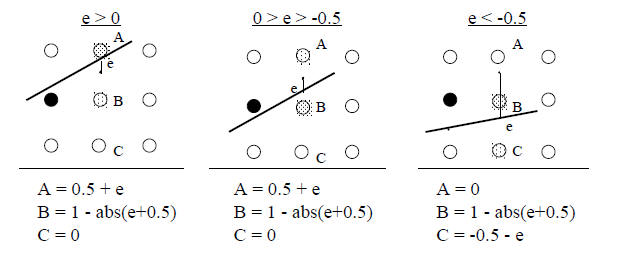
What about color?