Math 4650 Midterm Exam 1 Solutions
1. Use Horner's scheme to evaluate
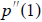 where p(x) = x3 - 2x2 + 5.
where p(x) = x3 - 2x2 + 5.
Solution : Horner's scheme becomes in this case as
follows (note that you must insert a zero entry
for the missing x- term ):
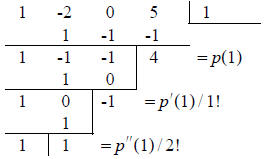
From the bottom row, we read off
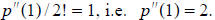
2. The function g(x) = ex - 2 has a fixed point near x =
1.146. Determine if the iteration
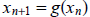 will converge or diverge if
will converge or diverge if
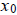 is located near this point.
is located near this point.
Solution : Since
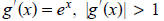 near the fixed point x ≈ 1.146 This implies that the fixed
near the fixed point x ≈ 1.146 This implies that the fixed
point iteration diverges near to it.
3. The figure to the right displays the function
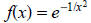 near the origin. Its only root is
near the origin. Its only root is
located at x = 0.
a. Determine the value of the constant c
with the property that Newton 's method
will converge to the root if |x0| < c and
diverge away from it if |x0| > c.
b. When Newton's method converges for
this function, determine weather the
convergence rate will be linear , or not?
Solution: Differentiating
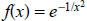 gives
gives 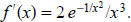 Newton's iteration
Newton's iteration
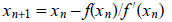 therefore takes the form
therefore takes the form
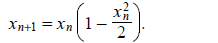 (1)
(1)
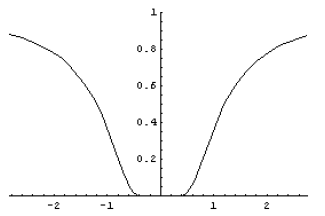
a. Looking at the illustration of
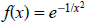 , it is clear that the break
point between
, it is clear that the break
point between
convergence and divergence will occur when 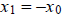 (causing an oscillation in
the
(causing an oscillation in
the
iterates that will remain of equal magnitude forever). In this case, the
relation (1) gives
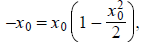 i.e.
i.e. 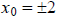 and c = 2.
and c = 2.
b. Linear convergence requires that
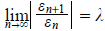 with
with 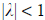 . Since the present root is
. Since the present root is
located at x = 0, we have (in view of (1)) 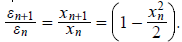 This limit is equal to
This limit is equal to
one, violating the requirement 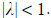 Hence, the convergence is NOT linear.
Hence, the convergence is NOT linear.
4. Multiple choice - for each question, mark below by a cross either True or
False (i.e. not always
correct). You do not need to give any explanations for your answers to this
problem.
| True | False | |
a. If the error n in an iterative process satisfies
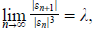 then the order of convergence is 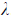 . . |
□ | ■ |
| b. The bisection method for solving f (x) = 0 requires f(x) to be differentiable (i.e. requires that f'(x) exists). |
□ | ■ |
| c. Müller's method is quadratically convergent . | □ | ■ |
| d. Aitken's method will turn a linearly convergent sequence into a quadratically convergent one. |
□ | ■ |
| e. Steffensen's method, when applied to the fixed point scheme in Problem 2 above, will produce quadratic convergence. |
■ | □ |
| f. Horner's scheme is also known as synthetic division . | ■ | □ |
| g. In the case of a simple root , Laguerre's method converges with order four . |
□ | ■ |
h. The matrix
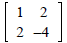 is singular. is singular. |
□ | ■ |
| i. A triangular matrix can always be inverted. | □ | ■ |
| j. The vector norms ||x||1 and ||x||2 are 'equivalent'. | ■ |   □ □ |
| Prev | Next |