Real Analysis I: Hints for Problems of Chapter 3
Section 3.1
3. Assume that f(x) is continuous. We want to show that |f(x)|
is also continuous. Let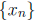 
be a sequence
that converges to x. Then by definition of continuity,
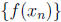converges to f(x). But then
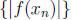converges
to |f(x)|. Hence |f(x)| is continuous.
4. Let f(x) = ln(sin x). Then x ∈ Dom(f) if and only if sinx > 0 if and only if
x∈ [2nπ , (2n + 1)π ] where
n = 0, 1, 2, · · · .
5. Suppose f is continuous and f(x) = 0 for x ∈ Q. We want to show f(x) = 0 for
all x. Let x ∈ R.
If x is a rational number , then f(x) = 0 by assumption. If x is not a rational
number, then for each n ∈ N,
we can choose a rational number
between x and x + 1/n. ( Draw a number line to
show this.) But then
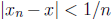and hence
converges to x. By
continuity of f we conclude that 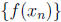converges to f(x),
that is,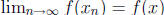 
. Since
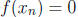for all n, we see that the limit
is also 0. Thus f(x) = 0.
6. If f is defined only on integers and a is an integer, then there is no
sequence of integers converging
to a for which 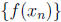does not converge to f(a). (In other words there is no
sequence for which the definition
of continuity fails)
7. Let f(x) = 3x - 1. Then |(fx) - 2| ≤ ε if and only if |3x - 1 - 2| ≤ ε if and only if
|3x -3| ≤ ε if and
only if |x - 1| ≤ ε /3. Thus we can choose
≤ ε /3.
8. Let f(x) = x2.
a) |x2 - 1| ≤ ε iff |x + 1||x - 1|≤ ε . If we choose x so that |x
- 1| ≤1, then x is
between 0 and 2 and
hence x + 1 is between 1 and 3. Thus, for this choice of x, we have |x2
- 1| =
|x + 1||x - 1| ≤ 3|x - 1|. To
make |x2 - 1| ≤ ε , all we need to do is make 3|x - 1| ≤ ε and for this we need |x
- 1| ≤ ε
/3. Thus we may
choose = min{1, ε /3}.
b) To make |x2- 4| ≤ ε , we note that |x2-4| = |x+2||x-2|. As in (a) above, choose x
so that |x-2| ≤1.
( Draw a number line for all such x.) Then |x + 2| ≤ 5. Therefore, |x2
- 4| = |x +
2||x - 2| ≤ 5|x - 2|. If
|x - 2| ≤ ε /5, then |x2 - 4| ≤ ε. Thus we choose
= min{1, ε/5}.
c) 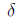gets smaller.
9. Let f(x) = 3x3 - 2. Let ε > 0 be given. |f(x) - 1| = |3x3
- 3| ≤ ε iff 3|x3 - 1| ≤ ε.
We now factor
x3-1 = (x-1)(x2+x+1) and estimate x2+x+1 assuming |x-1|
≤1. Note that |x-1| ≤1
implies 0 ≤ x ≤ 2 and
hence 0 ≤ x2 ≤ 4. Thus, if |x-1| ≤1, then 1 ≤ x2+x+1≤ 7. Now |f(x)-1|
≤ 3|x-1||x2+x+1|
≤ 3·7|x-1| ≤ ε
iff |x - 1|≤ ε /21. We can choose =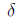
min{1, ε /21}.
10. Let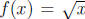 
. Let ε > 0 be given. First let c > 0. We now assume that |x
- c| ≤ c/2. ( Draw a
number a line to see the interval.) Then c/2 ≤ x ≤ 3c/2 and hence
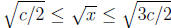. Adding 
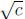to all
sides and taking the reciprocal , we get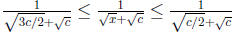 
. We now use this in the hint given:
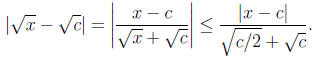
We can choose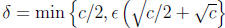 
(why?). For part(b), if c = 0, let 
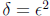. (Verify that this works!)
Section 3.2
1. If f(x) = x3 − 4x + 2, then f is continuous on [0, 1] and f(0) = 2 > 0 while
f(1) = −1 < 0. Then by
IVT, there exists a number c ∈ [0, 1] such that f(c) = 0. Thus f(x) hasa
zero in the indicated interval.
2. Let f(x) = ax3 + bx2 + cx + d be a cubic polynomial with a
≠ 0. If a > 0, then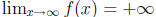 
and
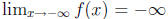. Thus there exist positive numbers M and N such that f(−M) < 0
and f(N) > 0. By
IVT, there exists a number y ∈ [−M,N] such that f(y) = 0. What happens if a < 0?
3. Assume that f is continuous on [a, b] and f(x) > 0 for all x. We want to show
that there exists
α
> 0 such that f(x) >α for all x. Suppose such a number does not exist. Then for
each positive integer n
(taking α = 1/n), there must be a number 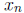in [a, b] such that
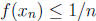. But then
is a sequence in
[a, b] and hence it is a bounded sequence. By Bolzano-Weierstrass Theorem, it
has a convergent subsequence,
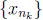that converges to a point x in [a, b]. (Why should x be in [a, b]? See
Problems 2.1 #7) But then
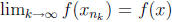by continuity of f. On the other hand
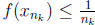and hence 
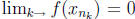. This
means that f(x) = 0, which is a contradiction. (To what?)
5. Assume f and g are continuous on [a, b] and f(x) < g(x) for all x. We want to
show that there exists
α
< 1 such that f(x) ≤ αg(x) for all x. Suppose such a number does not exist. Then
for each positive
integer n (taking α = 1- 1/n), there must be a number
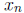in [a, b] such that
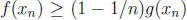. But
then is a sequence in [a, b] and hence it is a bounded sequence. By
Bolzano-Weierstrass Theorem, it has
a convergent subsequence, 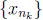that converges to
a point x in [a, b]. But then 
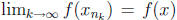and
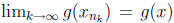by continuity of f and g. On the other hand,
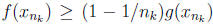and hence
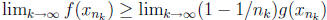. This means that f(x) ≥ g(x), which is
a contradiction.
6. For (a), let f(x) = x3 - 3x + 1, a = -2, b = 2, c = 0, and d = 1.
Verify that f(-2) < 0 < 1 < f(2).
Draw the graph to see that S is not one interval but rather a union of three
intervals.
For (b), we note that by IVT, there are two numbers
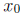and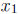 
in
[a, b] such that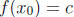 
and
.
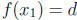Now show that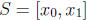 
. Here we must use the fact
that the function is increasing.
7. Let f be Lipschitz continuous on S. We want to show that f is uniformly
continuous on S. Let ε > 0 be
given. Since f is Lipschitz continuous on S, there exists a constant K > 0 such
that |f(x) − f(c)| ≤ K|x − c|
for ALL x and ALL c. If we choose =ε /K, we note that for all x and all c, if |x
− c| ≤, then
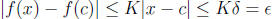. Therefore, f is uniformly continuous on S.
9. Let f(x) = 1/x. To show that f(x) is not uniformly continuous on (0,∞), we
need to find a positive
number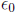 
and two sequences
and
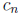such that
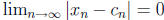but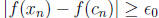 
. Let ε = 1/2,
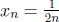, and 
.
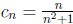Then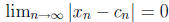 
because
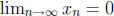and 
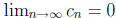. On the
other
hand, for n > 1, we have
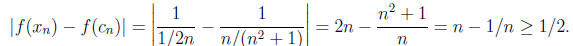
To show that f(x) = 1/x is uniformly continuous on [μ,∞), where μ > 0, we note
that if K = 1/μ2, then
for any x and any c in [μ,∞), we have x ≥ μ and c ≥ μ, and hence 1/x ≤ 1/μ and 1/c
≤ 1/μ. Thus,
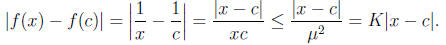
Thus f is Lipschitz and we apply #7 above.
| Prev | Next |