Example: 2x-1=y,2y+3=x
Sample Questions for Final Exam
Exercise 1
The pro t for a product is given by P(x) = 19x - 5060; where x is the
number of units produced and sold. The marginal pro t is defined to be
the slope of the line defining P(x): What is the marginal pro t? Interpret
the marginal pro t for this product.
Exercise 2
A company buys and retails baseball caps and the total cost function is linear .
The total cost for 200 caps is $2690, and the total cost of 500 caps is $3530.
Find the formula for the total cost function.
Exercise 3
The average rate of change of a function f(x) is defined by the difference
quotient
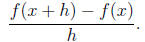
Find the average rate of change of the function f(x) = x2 + 1:
Exercise 4
The percent of high school seniors who smoke can be modeled by a linear
function p = f(t); where t is the number of years after 1975. Suppose that in
1981 the percent was 32.7 and in the year 2001 the percent was 32.1. Write
the equation of f(t):
Exercise 5
The average math SAT scores are given in the table below.
| Year | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 |
| Score | 472 | 464 | 470 | 471 | 473 | 470 |
(a) Construct a scatter plot with the x -value represent
the number of years
after 1990.
(b) Find the best linear t for this model .
Exercise 6
Suppose the daily demand for a product is given by p = 200 - 2q; where
q is the number of units demanded and p is the price per unit in dollars,
and that the daily supply is given by p = 60 + 5q; where q is the number
of units supplied and p is the price in dollars. If a price results in more
units being supplied than demanded, we say there is a surplus, and if the
price results in fewer units being supplied than demanded, we say there is a
shortfall. Market equilibrium occurs when the supply quantity is equal
to the demand quantity.
(a) If the price is $140, how many units are supplied and how many are
demanded?
(b) Does the price give a surplus or a shortfall of the product?
(c) What price give market equilibrium?
Exercise 7
If 200 feet of fence are used to enclose a rectangular pen, the resulting area
of the pen is A = x(100 - x); where x is the width of the pen. What is the
maximum possible area of the pen?
Exercise 8
The monthly total revenue for a product is given by R(x) = 300x - 0:01x2
dollars, where x is the number of units sold.
(a) To maximize the monthly revenue, how many units must be sold?
(b) What is the maximum possible monthly revenue?
Exercise 9
If a ball is thrown upward at 96 ft per second from the top of a building that
is
100 feet high, the height of the ball can be modeled by S(t) = 100+96t -16t2
feet, where t is the number of seconds after the ball is thrown.
(a) Describe the graph of the model .
(b) Find the t- coordinate and S -coordinate of the vertex of the graph of
this quadratic function .
(c) Explain the meaning of the coordinated of the vertex for this model .
Exercise 10
The total revenue function for a product is given by R(x) = 266x; and the
total cost is C(x) = 2000+46x+2x2; where x is the number of units produced
and sold. The revenue and cost are measured in thousands of dollars.
(a) Find the formula for the pro t function P(x):
(b) What is the pro t when 55 units are produced and sold?
(c) How many units must be sold to break even?(i.e. zero pro t)
Exercise 11
Consider the following set of data
| x | y |
| 17.6 26.0 31.9 38.9 45.8 51.2 58.1 64.7 66.7 80.8 82.9 |
159.9 206.9 236.8 269.9 300.6 323.6 351.7 377.6 384.1 437.2 444.7 |
(a) Graph a scatter plot.
(b) Find the best power function t.
(c) Graph the best power t and the scatter plot on the same window.
Exercise 12
Consider the following set of data
| x | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 6 | -1 | -3 | -1.5 | 5 | 10 |
(a) Graph a scatter plot.
(b) Find the best quadratic t.
(c) Graph the best quadratic t and the scatter plot on the same window.
Exercise 13
(a) Graph the function f(x) = 2x3 - 1:
(b) Does the function have an invers? If yes, find the expression for f-1(x):
Exercise 14
If x dollars are invested at 10% for 6 years, the future value of the investment
is given by S(x) = 1:06x:
(a) Find the inverse of this function.
(b) What do the outputs of the inverse function represent?
(c) Use this function to find the amount of money that must be invested for
6 years at 10% to have a future value of $24,000.
Exercise 15
It pays to advertise, and it is frequently true that weekly sales will drop
rapidly for certain products after an advertising campaign ends. This decline
is called sales decay. Suppose that the decay in the sales of a product is
given by
S(x) = 1000 2-0.5x dollars
where x is the number of weeks after the end of a sales campaign. Use this
function to answer the following.
(a) What is the level of sales when the advertising campaign ends?
(b) What is the level of sales one week after the end of the campaign?
Exercise 16
If $8,000 is invested for t years at 8% interest compounded continuously , teh
future value is given by S(t) = 8000e0.08t dollars. Find the doubling time,
that is, the time it takes for the investment to reach $8,000.
Exercise 17
If $10,000 is invested for 15 years at 10%, compounded continuously, what is
the future value of the investment?
Exercise 18
Solve: 2 log x - 2 = log (x - 25).
Exercise 19
Solve: 18, 000 = 30(2)12x.
Exercise 20
The write the following expression as a single logarithm: 3 ln x + ln y.
Exercise 21
Solve: 5 + 2 ln x = 8.
Exercise 22
Find the exponential function that models the data in the table below.
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 2/9 | 2/3 | 2 | 6 | 18 | 54 | 162 | 486 |
Exercise 23
Find the logarithmic function that models the data in the table below.
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 2 | 4.08 | 5.3 | 6.16 | 6.83 | 7.38 | 7.84 |
Exercise 24
The table below gives the annual premiums required for a $250,000 20-year
term-life insurance policy in female nonsmokers of different ages . Find an
exponential function that models the monthly premium as a function of the
age of the female nonsmoking policyholder.
| Age | 35 | 40 | 45 | 50 | 55 | 60 | 65 | 70 | 75 |
| Monthly Premium | 145 | 185 | 253 | 363 | 550 | 845 | 1593 | 2970 | 5820 |
Exercise 25
The percent of persons over age 18 who are smokers for selected years between
1965 and 1995 is given in the table below.
(a) Find a logarithmic function that models the data, using an input equal
to the number of years after 1960.
(b) Use the model to estimate the percent of smokers in 1989.
| Year 1965 1974 1979 1983 1985 1987 1990 1991 1992 1993 1994 1995 |
Smokers (%) 42.4 37.2 33.5 32.2 30.0 28.7 25.4 25.4 26.4 25.0 25.5 24.7 |
Exercise 26
If $5,500 is invested for t years at 12% interest compounded quarterly, the
future value that results is S = 500(1:03)4t. Find the time when the money
will double in value.
Exercise 27
If $10,000 is invested at 12% interest compounded quarterly, find the future
value in 10 years.
Exercise 28
If $10,000 is invested at 12% compounded monthly, find the interest earned
in 15 years.
Exercise 29
The revenues (in thousands of dollars) of Holiday Inn for the years 1995-1999
are given in the table below.
| Year | Revenue |
| 1995 | 51,962 |
| 1996 | 68,342 |
| 1997 | 62,666 |
| 1998 | 68,618 |
| 1999 | 76,058 |
(a) Find the quartic model that is the best t for this
data, with y equal to
the revenue in thousands of dollars and x equal to the number of years after
1995.
(b) Use the model to estimate the revenue in 1998 and compare it with the
data in the table.
Exercise 30
The data in the following table list natural gas consumption ( in quadrillion
BTU) in the United States.
| Year | 1960 | 1970 | 1980 | 1990 | 1997 |
| Consumption | 12.4 | 21.8 | 20.4 | 19.3 | 22.6 |
(a) Find a polynomial function of degree 3 that models the
data.
(b) Graph f and the data together.
(c) Estimate the natural gas consumption in 1982.
Exercise 31
The table shows how the average age of the first marriage of Japanese women
varied in the last half of the 20th century.
| Year | Average Age | Year | Average Age |
| 1950 | 23.0 | 1975 | 24.7 |
| 1955 | 23.8 | 1980 | 25.2 |
| 1960 | 24.4 | 1985 | 25.5 |
| 1965 | 24.5 | 1990 | 25.9 |
| 1970 | 24.2 | 1995 | 26.3 |
(a) Find a polynomial function of degree 4 that models the
data.
(b) Graph f and the data together.
(c) Estimate the average age in 1987.
Exercise 32
Solve the equation by factoring: x4 - 3x3 + 2x2 = 0:
Exercise 33
Solve the equation using the factoring by grouping: 4x3 - 8x2 - 36x - 72 = 0:
Exercise 34
Solve the equation graphically: 4x3 - 15x2 - 31x + 30 = 0:
Exercise 35
The revenue from the sale of a product is given by the function R(x) =
400x - x3. Use factoring to find the number of units that must be sold to
give zero revenue.
Exercise 36
Solve graphically the equation: -2.56x3 + 53.73x2 - 356.47x + 757.74 = 0:
Exercise 37
Solve:
(a) x3 + 27 = 0
(b) 5x4 = 80
(c) x2 + 1 = 0:
| Prev | Next |