Math Exam 1 Solutions
1) (20 points) Consider the following system of linear equations :
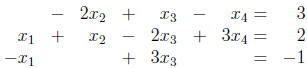
a) Write the augmented matrix for this system.
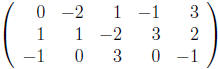
b) Reduce the system to Reduced Echelon Form.
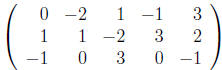.Switch R1 and R2
.
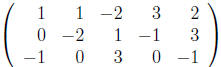Eliminate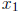 
from 2nd and 3rd row (R1 + R3)
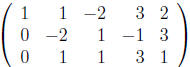. Switch R2 and R3
.
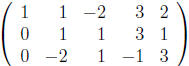Eliminate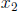 
from third row (R3 + 2R2):
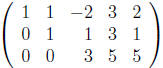. Make leading entry in
third row 1 (R3/3) 
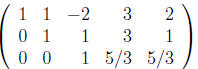
Eliminate 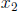from first row: (R1 − R2):
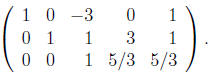
Eliminate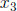 
from first and second row (R1 + 3R3 and R2 −
R3):
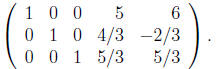
c) Find the general solution to this system of equations.
From the reduced echelon form we see that the system reduced to the following
equations:
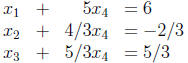
Therefore the general solution is :
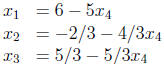
where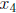 
is an independent variable and can take any
value.
d) Write the general solution in vector form.
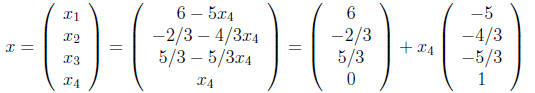
2) (20 points) Let
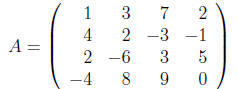
and
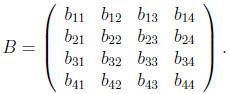
a) Find the third column of AB.
The third column of AB comes from multiplying A by the third column of B:
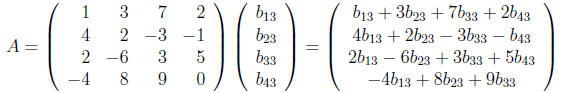
b) Find (AB)34 (the entry of AB in third row and fourth
column).
AB34 comes from multiplying third row of A by fourth column of B:
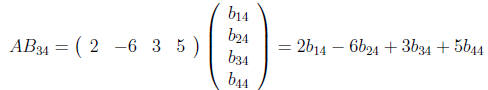
c) Let C be a non-singular 4x4 matrix with rows
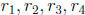. Let the columns of C-1 be
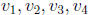. Calculate
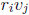for 1≤ i, j ≤ 4.
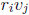is the entry in i-th row and j-th column of CC-1. We know that CC-1 = I4
the 4x4
identity matrix. Therefore 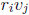= 1 when i = j and
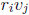= 0 when i ≠ j.
3)(20 points) Determine whether the vectors
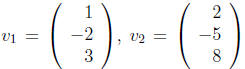and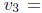 
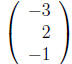are linearly dependent or linearly
independent. If the vectors are linearly dependent,
express 0 as a nontrivial linear combination of the vectors .
In order to find out whether vectors are linearly dependent we need to find all
of their
linear combinations that equal 0:
.
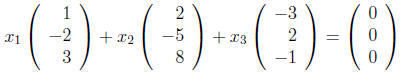
This is the same as finding all of the solutions of:
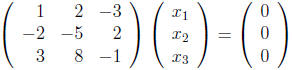
The augmented matrix of this system is:
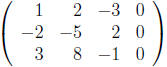
We reduce it to reduced echelon form: (R2 + 2R1 and R3 − 3R1)
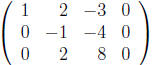
Now we eliminate
from the third row: (R3 + 2R2)
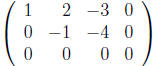
We make the leading entry in second row 1 (−R2) and use
second row to eliminate
from
the first row:
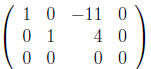
The general solution is:
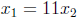and 
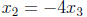with
an independent variable. Since
there are infinitely many solutions the vectors are linearly dependent . To find
a particular
nontrivial combination we need to pick a value of
. Lets
choose = 1. Then x=11 and
= −4 and the linear combination is:
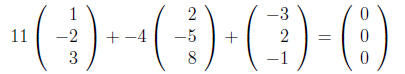
4) (20 points) Find all of the values of a such that the matrix
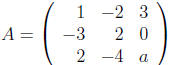
is singular. Briefly explain your reasoning.
In order to find out of A is singular we need to find all of the solutions to Ax
= 0. We begin
by reducing the augmented matrix to echelon form:
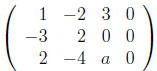
We eliminate
from the second and third row: (R2 + 3R1
and R3 − 2R2
.
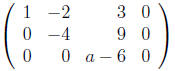
When a ≠ 6 it follows that
= 0 and then from row 2
= 0 and then
= 0.
Thus when
a ≠ 6 the only solution to Ax = 0 is x = 0 and therefore A is nonsingular.
When a = 6 we have the system:
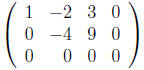
Here
is an independent variable and thus there are
infinitely many solutions to Ax = 0.
Therefore when a = 6 the matrix A is singular and A is nonsingular for any other
value of a.
5) (20 points) a) Find one example of a nonsingular 4x4
matrix A that satisfies A2 = A.
I4 the 4x4 identity matrix is nonsingular and I2 = I.
b) Find all 4x4 nonsingular matrices that satisfy A2 = A. Explain your
reasoning.
Since A is nonsingular A has an inverse matrix A-1. We can multiply both sides
of the
equation by A -1:
A-1A2 = A-1A which means that IA = I and therefore A = I. Thus the identity
matrix
is the only 4x4 nonsingular matrix that satisfies A2 = A.
| Prev | Next |