Linear Algebra

1 Subspaces

Definition 2.1. A subset U 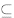V is a subspace (written U ≤ V ) if



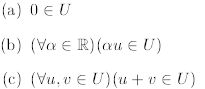
Exercise 2.2. Show 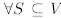, Span(S) ≤ V , i.e. that Span(S) is a subspace of V . (Recall
that .)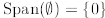

Exercise 2.3. Show that Span(S) is the smallest subspace containing S, i.e.

(a) Span(S) ≤ V and Span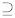(S) S:

(b) If W ≤ V and S W then Span(S) ≤ W:

Corollary 2.4. .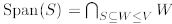

Exercise 2.5. Show that the intersection of any set of subspaces is a subspace.

Remark 2.6. Note that this doesn't hold true for unions.

Exercise 2.7. If then 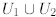is a subspace if and only if 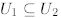or .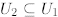

2 All bases are equal

Theorem 2.8 (Fundamental Fact of Linear Algebra ). If L ,M V with L is a linearly
independent set of vectors, and L ≤ Span(M) then lLl ≤ lMl.

Lemma 2.9 (Steinitz Exchange Principle). If 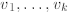are linearly independent and
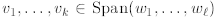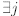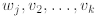then , 1≤ j ≤ l such that are linearly indepen -
dent. (Note in particular that .)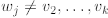

Exercise 2.10. Prove the Steinintz Exchange Principle.

Exercise 2.11. Prove the Fundamental Fact using the Steinitz Echange Principle.

Definition 2.12. An m × n matrix is an m × n array of numbers 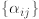which we write as

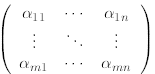
Definition 2.13. The row (respectively column) rank of a matrix is the rank of the set
of row (respectively column) vectors.

Theorem 2.14 (The Most Amazing Fact of Basic Linear Algebra ). The row rank of
a matrix is equal to its column rank. (To be proven later in today.)

Definition 2.15. Let S V , then a subset B S is a basis of S if

(a) B is linearly independent .

(b) S ≤ Span(B).

Exercise 2.16. Show that the statement: "All bases for S have equal size" is equivalent
to Theorem ??.

Definition 2.17. We call the common size of all bases of S the rank of S, denoted rk(S).

3 Coordinates

Exercise 2.18. Show that B S is a basis if and only if B is a maximal linearly independent
subset of S.

Exercise 2.19. If B is a basis of S then there exists a unique linear combination of
elements in B that sums to x . In other words for all x there are unique scalars 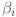such that

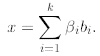
Definition 2.20. For a basis B, regarded as an ordered set of vectors, we associate to each
x ∈S the column vector

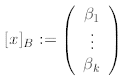
called the coordinates of x , where the are as above.

4 Linear maps, isomorphism of vector spaces

Definition 2.21. Let V and W be vector spaces. We say that a map f : V → W is a
homomorphism or a linear map if



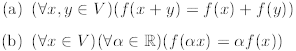
Exercise 2.22. Show that if f is a linear map then f(0) = 0.

Exercise 2.23. Show that .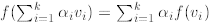

Definition 2.24. We say that f is an isomorphism if f is a bijective homomorphism.

Definition 2.25. Two spaces V and W are isomorphic if there exists an isomorphism be-
tween them.

Exercise 2.26. Show the relation of being isomorphic is an equivalence relation.

Exercise 2.27. Show that an isomorphism maps bases to bases.

Theorem 2.28. If dim(V ) = n then .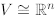

Proof: Choose a basis, B of V , now map each vector to its coordinate vector, i.e. v → [v]B.

Definition 2.29. We denote the image of f as the set



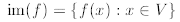
Definition 2.30. We denote the kernel of f as the set



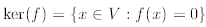
Exercise 2.31. For a linear map f : V → W show that im(f) ≤ W and ker(f) ≤ V .

Theorem 2.32. For a linear map f : V → W we have

dim ker(f) + dim im(f) = dim V.

Lemma 2.33. If U ≤ V and A is a basis of U then A can be extended to a basis of V .

Exercise 2.34. Prove Theorem ??. Hint: apply Lemma ?? setting U = ker(f).

5 Vector spaces over number fields

Definition 2.35. A subset F C is a number field if F is closed under the four arithmetic
operations, i.e. for ,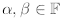



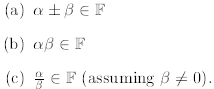
Exercise 2.36. Show that if F is a number field then Q F.

Exercise 2.37. Show that 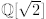is a number field.

Exercise 2.38. Show that 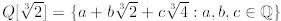is a number field.

Exercise 2.39 (Vector Spaces over Number Fields). Convince yourself that all of the
things we have said about vector spaces remain valid if we replace R and F.

Exercise 2.40. Show that if F,G are number fields and F G then G is a vector space over
F.

Exercise 2.41. Show that .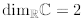

Exercise 2.42. Show that 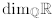has the cardinality of "continuum," that is, it has the same
cardinality as R.

Exercise 2.43 (Cauchy' s Equation ). We consider functions f : R → R satisfying Cauchy's
Equation: f(x + y) = f(x) + f(y) with x, y ∈ R. For such a function prove that

(a) If f is continuous then f(x) = cx.

(b) If f is continuous at a point then f(x) = cx.

(c) If f is bounded on some interval then f(x) = cx.

(d) If f is measurable in some interval then f(x) = cx.

(e) There exists a g : R → R such that g(x) ≠ cx but g(x + y) = g(x) + g(y). (Hint: Use
the fact that R is a vector space over Q. Use a basis of this vector space. Such a basis
is called a Hamel basis.

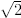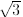Exercise 2.44. Show that 1,, and are linearly independent over Q.

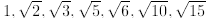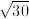Exercise 2.45. Show that and are linearly independent over
Q.

Exercise 2.46. *Show that the set of square roots of all of the square-free integers are linearly
independent over Q. (An integer is square free if it is not divisible by the square of any prime
number. For instance, 30 is square free but 18 is not.)

Definition 2.47. A rational function f over R is a fraction of the form



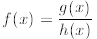
where g, h ∈ R[x] (that is g, h are real polynomials ) and h(x) ≠ 0 (h is not the identically
zero polynomial ). More precisely , a rational function is an equivalence class of fractions of
polynomials , where the fractions 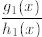and 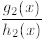are equivalent if and only if .
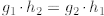(This is analogous to the way fractions of integers represent rational numbers, the fractions
3/2 and 6/4 represent the same rational number.) We denote the set of all rational functions
as R(x).

Note that a rational function is not a function, it is an equivalence class of formal quotients.
Exercise 2.48. Prove that the rational functions 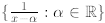are linearly independent set
over R(x).

Corollary 2.49. 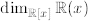has the cardinality of "conyinuum" (the same cardinality as R).

6 Elementary operations

Definition 2.50. The following actions on a set of vectors 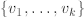are called elementary
operations:

(a) Replace 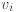by 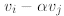where i ≠ j.

(b) Replace 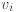by 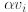where α ≠ 0.

(c) Switch 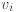and .

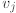Exercise 2.51. Show that the rank of a list of vectors doesn't change under elementary
operations.

Exercise 2.52. Let 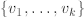have rank r. Show that by a sequence of elementary operations
we can get from 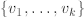to a set 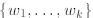such that 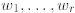are linearly independent
and .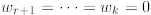

Consider a matrix. An elementary row-operation is an elementary operation applied
to the rows of the matrix. Elementary column operations are defined analogously. Exercise ??
shows that elementary row-operations do not change the row-rank of A.

Exercise 2.53. Show that elementary row-operations do not change the column-rank of
a matrix.

Exercise 2.54. Use Exercises ?? and ?? prove the "amazing" Theorem ??.