Solving Equations:The Addition Principle
Solving Equations : The Addition Principle
EQUATIONS AND SOLUTIONS
Solving equations is very important to be able to solve word problems. We begin
solving equations in this section.

Problem 1
Determine whether the given number is a solution of the given equation.

USING THE ADDITION PRINCIPLE
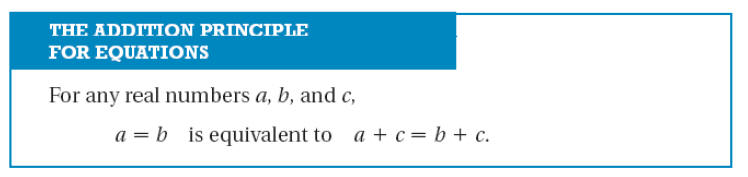
In other words, whatever “we” do to one side must be
performed to the other side as
well. You may add some number to both sides or you may subtract (since
subtraction is
really addition of the opposite) to both sides.
Problem 2
Solve the following equations.
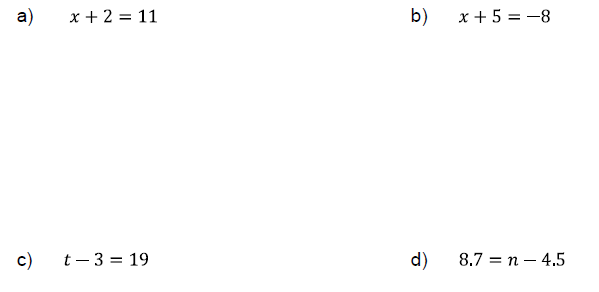
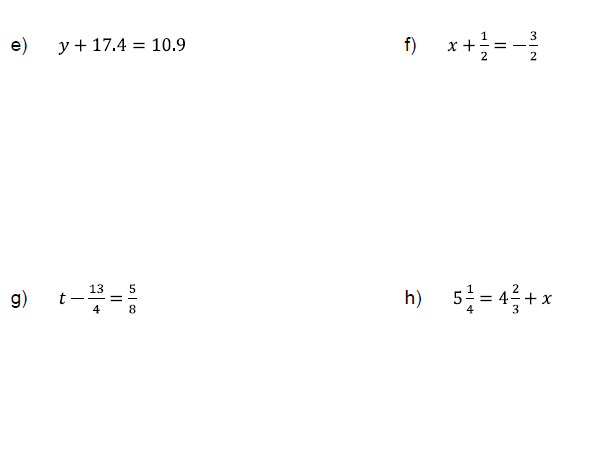
Section 10.2 – Solving Equations: The Multiplication Principle
USING THE MULTIPLICATION PRINCIPLE

In the previous section we introduced the addition principle which means you can “add” or “subtract” any number from “both sides” of the equation. Well, that holds true as well for “multiplication” and “division”.
Problem 1
Solve the following equations.
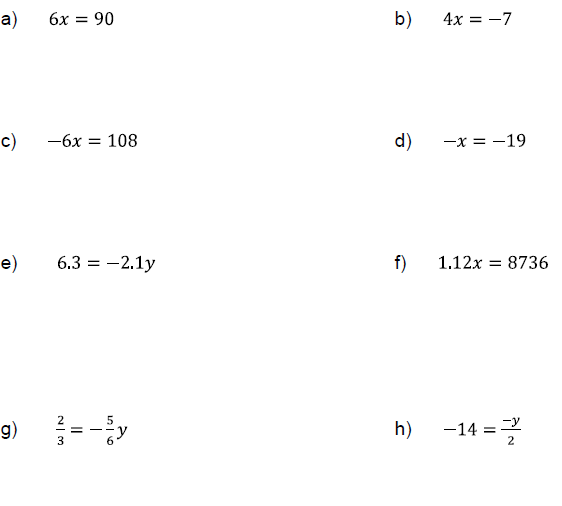
Section 10.3 – Using the Principles Together
In all honesty, most equations require more than one step to solve . So, we will have to use all of the principles together at one time or another. Remember your goal is to isolate the variable.
Problem 1
Solve the following equations.
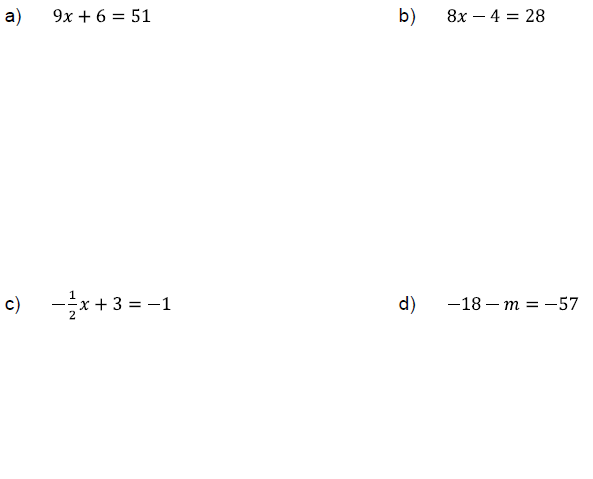
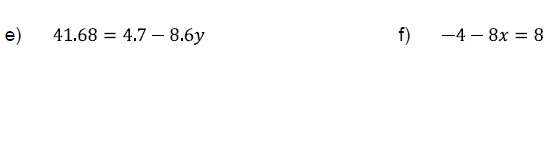
COLLECTING LIKE TERMS
If there are like terms on one side of the equation, we collect them before
using the addition or the multiplication principle.
Problem 2
Solve the following equations.
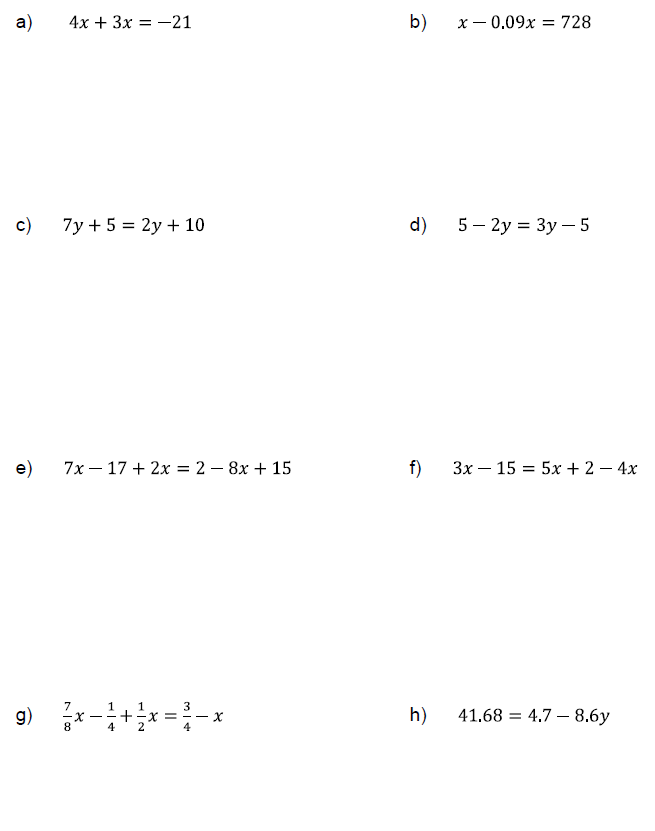

EQUATIONS CONTAINING PARENTHESES
To solve certain kinds of equations that contain parentheses , we first use the
distributive laws to remove the parentheses. Then we solve as before.
Problem 3
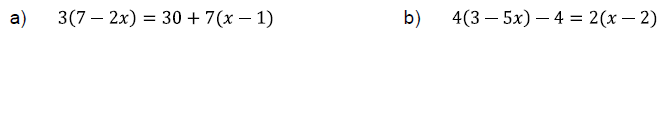
EQUATIONS WITH INFINITELY MANY SOLUTIONS
Not all equations have exactly one solution like the ones we have encountered so
far. Some equations have an infinite number of solutions. We will study them
now.
Problem 4
Determine whether the given number is a solution of the given equation.
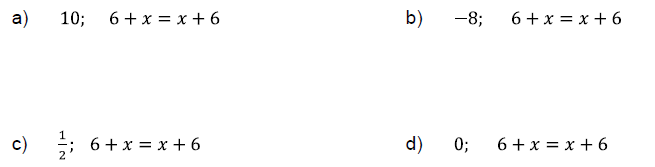
EQUATIONS WITH NO SOLUTION
As mentioned earlier not all equations have only one solution. We learned that
some equation have an infinite number of solutions. Furthermore, there are some
equation that have no solution.
Problem 5
Determine whether the given number is a solution of the given equation.
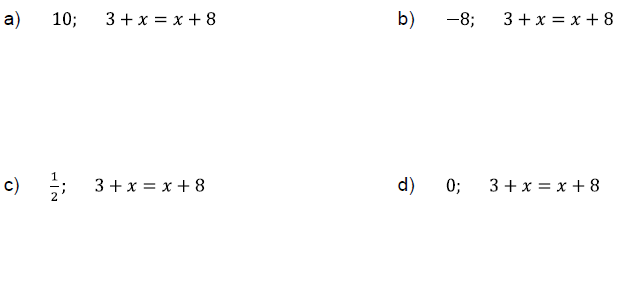
Problem 6
Solve the following equations.
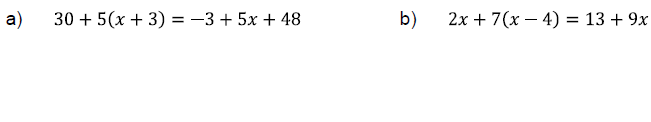
| Prev | Next |