Simplifying Rational Expressions
By the end of this section, you should be able to solve the following problems.
1. Write the rational expression in lowest terms.
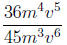
2. Simplify the rational expression .
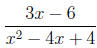
3. Simplify the rational expression .
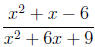
4. Simplify the rational expression.
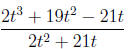
2 Concepts
Any rational expression is completely simplified when
there are are no common
factors in its numerator and denominator. For example, the fraction ,
18/12 , can be simplified because the numerator and denominator share a common
factor of 6. In general, any ratio of the form
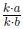 where (k, b ≠ 0) can
where (k, b ≠ 0) can
be reduced. The following examples will illustrate how to reduce rational
expressions.
3 Example
1. Reduce the expression to lowest terms .
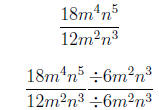
=
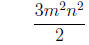
2. Reduce to lowest terms .
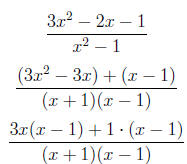
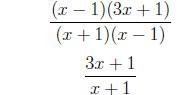
3. Reduce to lowest terms.
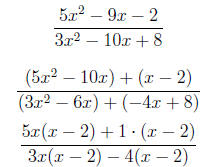
=
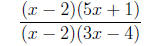
=
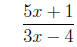
4 Facts
1. Any rational expression is completely simplified when
their are no factors
in common between the numerator and denominator.
2. Always make sure the numerator and denominator are
completely factored
before you do any cancellation. You must always have pure mul-
tiplication in the numerator and denominator before reducing. Never
cancel across addition .
5 Exercises
1. Write the rational expression in lowest terms.
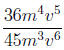
2. Simplify the rational expression.
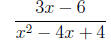
=
3. Simplify the rational expression.
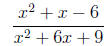
=
4. Simplify the rational expression
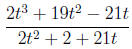
1. Write the rational expression in lowest terms.
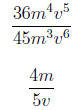
2. Simplify the rational expression.
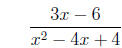
=
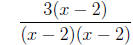
=
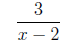
3. Simplify the rational expression.
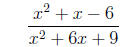
=
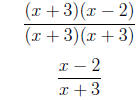
4. Simplify the rational expression
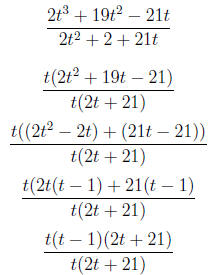
=
t − 1
| Prev | Next |