INTEGER AND RATIONAL NUMBERS
Theorem 7.10 Both the integers and the rational numbers are countable.
Proof By Theorem 4.4 we know that N × N is countable. there exists the
natural embedding of Z into N × N by identifying [a, b] with its canonical
representative (a-b, 0) or (0, b-a). Thus there exists a bijection from Z to
a subset of a countable set, hence Z is countable. Again by Theorem 4.4 we
know that Z × Z is countable, and there exists the natural embedding of Q
into Z×Z by identifying [a, b] with its canonical representative, (c, d) where
d is positive and minimal . Thus there exists a bijection from Q to a subset
of a countable set, hence Q is countable.
Let Z* represent the image of the embedding of Z into Q. Also let
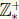
and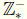 
represent respectively the images of the embeddings of the positive
and negative integers into the rationals .
The Archimedian Property
Theorem 7.11 Archimedian Property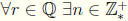 
such that r < n.
Proof Let r = [a, b], if r ≤ 1, then r < 2 and we are done. If r > 1, then
without loss of generality, both a, and b are positive integers , and
b(a + 1) ≥ a + 1 > a
=> [a, b] < [a + 1, 1] ∈ .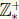
Lemma For positive rational numbers r and s, if r > s, then r -1 < s-1.
Proof First we note that if r = [a, b], then r -1 = [b, a],
this is immediate
by computing [a, b] · [b, a] = [ab, ab] = [1, 1]. Now let r = [a, b] and s = [c,
d].
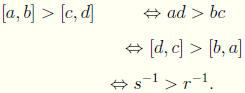
For any integer, a, the product of a with itself b times,
where b is a
positive integer is denoted ab.
Exercise Prove that for any positive integer, n, there exists an integer of
the form 2m for some positive integer m, such that 2m > n. (Hint: use
induction).
Solution For n = 1, 1 < 2 = 21. Now assume n < 2m for some m, then
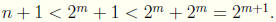
Exercise Prove that for any positive rational number, q, there exists a
rational number of the form 2n, where 2n > q, and where n is the embedded
image of a positive integer.
Solution Let q = (a, b) where a and b are positive integers. We then have
(a, b) ≤ (a, 1) < (2n, 1) for some n.
The Division Algorithm
Theorem 7.12 The division algorithm If a and d are integers with d > 0,
then there exist unique integers q and r such that a = dq +r and 0 ≤ r < d.
Proof This result is a consequence of the well ordering property.
Let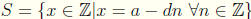 
, and let
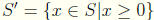, S' is thus
the embedded image of some subset of N, and thus if it is
non-empty it must
have a least element .
If a ≥ 0, then let n = 0, and thus x = a - 0 = a ≥ 0. Thus a ∈ S'. If
a < 0, then let n = a, thus x = a-ad = a(1-d) ≥ 0. Thus a-ad ∈ S'. Thus
S' ≠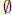 
. Since S' ≠ 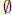, and is embedded image of a subset of N, S' has a least
element. Let the least element be r. Thus we have r = a - dq ≤ s
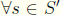
and a = dq + r where r ≥ 0.
We now must show r < d. We have a - d(q + 1) = a - dq - d = r - d,
thus r - d ∈ S. Since r is the least element in S' and r - d < r we have
r - d < 0 => r < d. We thus have a = dq + r with 0 ≤ r < d.
Now we have to show that q and r are unique. Suppose
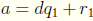and
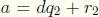where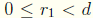 
and
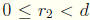. Without loss of generality
we may assume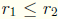 
. We thus have
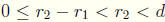. We note that
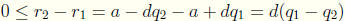. Thus 
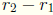is a multiple of d
and non -negative. We thus have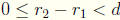 
and
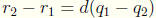
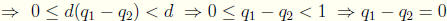. Thus 
,
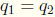and thus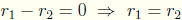 
.
Exercises
1. Verify that the relation (a, b) ≡ (c, d)
a+d = b+c is an equivalence
relation on N × N, but not on α × α where α > ω.
2. Verify that the relation (x, y) ≡ (z,w)
xw = yz is an equivalence
relation on Z × (Z - { 0 })
For any Integral Domain D show:
3. 
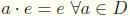and where e is the additive identity .
4. u · (-u) = -u, where u is the multiplicative identity .
5. (-u) · (-u) = u, where u is the multiplicative identity .
6. If a, z ∈ D and a + z = a, then show z = e.
Solution to 3: a = a · u = a · (u + e) = a + a · e => a · e = e:
7. If v, a ∈ F, where F is a field and a · v = a, then show v = u.
8. Show that every Field is an Integral Domain.
Mathematical Induction is often used to prove certain identities. Exer-
cise 9 and its solution exemplifies how this is done. Exercise 10 is left
as practice.
9. Show that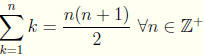 
Solution to 9: Let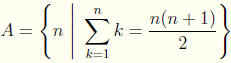 
i.
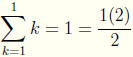thus 1 ∈ A.
ii. Assume m ∈ A, then
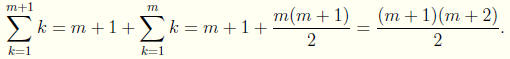
Thus m + 1 ∈ A. Therefore by Mathematical Induction A = N,
and
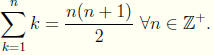
10. Show that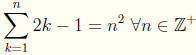 
:
| Prev | Next |