Math Homework Solution
7.5, #46. The integrand is an improper rational function . Long division gives
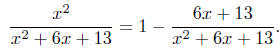
Completing the square gives x2 + 6x + 13 = (x +
3)2 + 22, so set w = x + 3 and dw = dx.
Then
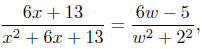
so formula 25 applies with a = 2, b = 6, c = -5, giving
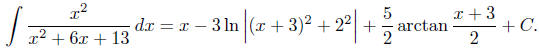
7.5, #50. The integrand is an improper rational function . Long division gives
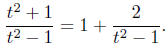
Since t2 - 1 = (t - 1)(t + 1), formula 26 with a = 1, b = -1 gives
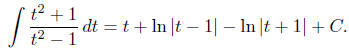
7.5, #51. Formula 24 with a = 2 gives
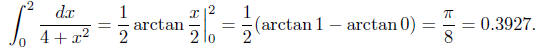
The left and right Riemann sums with n = 100 are
approximately 0.3939 and 0.3915. Since
the integrand is decreasing on the interval [0, 2], its value is between these
two estimates.
7.5, #53. Since x2 + 2x + 5 = (x + 1)2 + 22, formula 24 with a = 2 gives
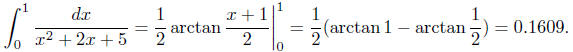
The left and right Riemann sums with n = 100 are
approximately 0.1613 and 0.1605. Since
the integrand is decreasing on the interval [0, 1], its value is between these
two estimates .
7.5, #64. (a) The average voltage over a second is
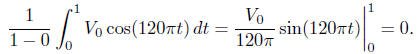
(b) The average of V 2 over a second is
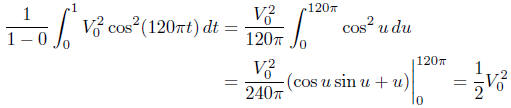
using the substitution u = 120πt and du = 120πdt. Thus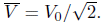
(c) If 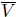 = 110, then V0
=
= 110, then V0
= 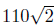 = 155.56 volts.
= 155.56 volts.
7.6, #1.
| n = 1 | n = 2 | n = 4 | |
| LEFT | 40.0000 | 40.7846 | 41.7116 |
| RIGHT | 51.2250 | 46.3971 | 44.5179 |
| TRAP | 45.6125 | 43.5909 | 43.1147 |
| MID | 41.5692 | 42.6386 | 42.8795 |
7.6, #3.
| n | 10 | 100 | 1000 |
| LEFT | 5.4711 | 5.8116 | 5.8464 |
| RIGHT | 6.2443 | 5.8890 | 5.8541 |
| TRAP | 5.8577 | 5.8503 | 5.8502 |
| MID | 5.8465 | 5.8502 | 5.8502 |
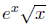 is increasing and
concave-up on [1, 2] since
is increasing and
concave-up on [1, 2] since
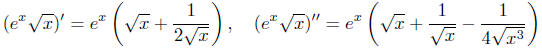
are positive on [1, 2]. (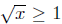 and
and 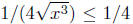 for
for 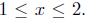 )
So LEFT and MID
)
So LEFT and MID
underestimate the integral, RIGHT and TRAP overestimate the
integral
7.6, #4.
| n | 20 | 100 | 1000 |
| LEFT | 3.0132 | 2.9948 | 2.9930 |
| RIGHT | 2.9711 | 2.9906 | 2.9925 |
| TRAP | 2.9922 | 2.9927 | 2.9927 |
| MID | 2.9930 | 2.9927 | 2.9927 |
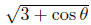 is decreasing and
concave-down on [0,
is decreasing and
concave-down on [0, 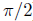 ] since
] since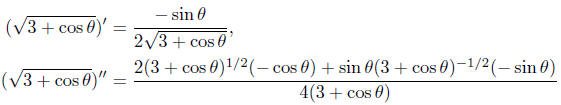
are negative on 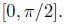 (The
second derivative is messy, but its sign is easy to determine.
(The
second derivative is messy, but its sign is easy to determine.
The numerator is always negative since square roots are non-negative; the
denominator
is positive for 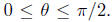 ) So LEFT and MID
overestimate the integral, RIGHT and
) So LEFT and MID
overestimate the integral, RIGHT and
TRAP underestimate the integral.
| Prev | Next |