Solving Equations

Instructions: Simplify the expression using the correct order of operations.
#1 2 + 2 × 4² - (12 - 3)

Instructions: Solve the following equations. Circle your answers.
#2 x + 7 = 19

#3 - 9x = 45

#4 12x - 6x + 8 = 32

#5 50x + 10 + 20x = 170 -10x

#6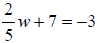

#7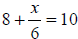

#8 x - (20 - 3x) = -8

#9 - 3(2x + 7) + 3x - 6 = 5x + (4x + 6 - x)

#10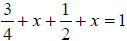

SOLUTIONS
Instructions: Simplify the expression using the correct order of operations.
#1

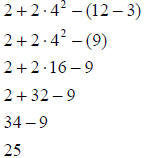	Perform operations in the parenthesis first .
	Apply exponents second .
	Perform multiplication/ division moving from left to right third
	Perform addition/ subtraction moving from left to right fourth.

Instructions: Solve the following equations . Circle your answers .

#2

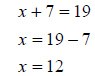Subtract 7 from both sides.

#3

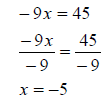Divide both sides by –9.

#4

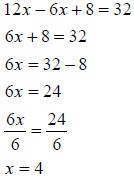	Combine the like terms , that is, the two terms with variable parts: 12x and –6x.
	Subtract 8 from both sides.
	Divide both sides by 6.

#5

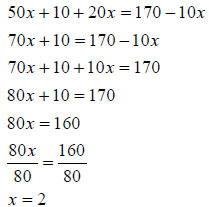	Combine the like terms . Start by combining like terms that are on the same side of the equation. In this equation, combine the 50x with the 20x.
	Now add 10x to both sides in order to combine all the terms with variable parts.
	Subtract 10 from both sides.
	Divide both sides by 80.

#6

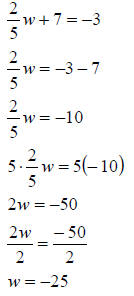	Subtract 7 from both sides.
	Multiply both sides by 5.
	Divide both sides by 2.

#7

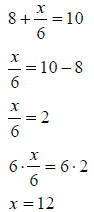	Subtract 8 from both sides.
	Multiply both sides by 6.

#8

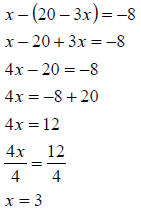	Distribute the negative across the binomial. Be sure to change the sign of each term of the binomial.
	Combine like terms, namely the x and 3x.
	Add 20 to both sides.
	Divide both sides by 4.

#9

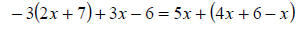	Distribute the –3 across the binomial on the left side of the equation.
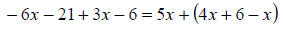	Combine the like terms in the parenthesis on the right side of the equation.
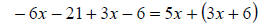	The parentheses can be dropped since the binomial is not being multiplied by any factor .
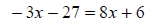	Combine the like terms on the right side of the equation: –6x + 3x = –3x.
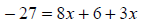	Combine like terms separated by the equal mark. Either add 3x to both sides or subtract 8x. This example adds 3x.
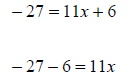	To isolate the variable, subtract 6 from both sides.
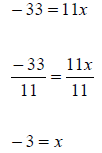	To isolate the variable, divide both sides by 11.

#10

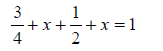	Combine like terms on the same side. Add x + x to get 2x.
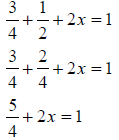	Add the two fractions together. Remember fractions must have a common denominator so change one-half to two-fourths then you can add it to three-fourths to get five-fourths.
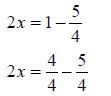	Subtract five-fourths from both sides. Again, remember that fractions must have a common denominator . Change the one to a fraction, 4/4, so that it can be added to 5/4.
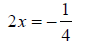	To isolate the variable, divide by 2. Or, multiply by the reciprocal , 1/2.
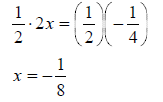	Multiplying by one-half will also isolate the variable.