Math 116 Exam #2
Suggestions: Read carefully. Write clearly and
unambiguously. Use separate lines for each equation. Leave some space
between lines . Write “ = ” signs only when needed. Clarity and precision will be
rewarded, messiness and imprecision will
be punished. Show all your work. Good Luck.
[20 pts] Question 1 ( Compare with HW # 10 - Sec 4.2 prob # 46)
Use the rational root theorem to find all zeros of p(x) =
7x3 - 15x2 + 3x - 2. Write your answer as a list. For instance, the
solution set is 2, 1, 5 . Do not use synthetic division ; use long division
instead. Also, make sure that you list all possible
rational zeros of p (x).
Solution. Assume there exists a rational zero of
the form b/c , then b must be a factor of -2, and c must be a factor of 7.
Hence b = ±1, ±2 and
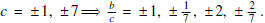Note that p(2) = 0, and thus x - 2 is a
factor. Now we
write p(x) = (x - 2)q(x) and we found q(x) by dividing p(x) by x - 2 to obtain
q(x) = 7x2 - x + 1. Now we find the zeros
of q(x) by the quadratic formula to obtain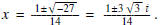 
Therefore, the solution set is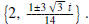 
[20 pts] Question 2 (Compare with HW # 10 -Sec 4.2 prob # 70)
Use the conjugate root theorem to find all zeros of p(x) =
x4 + 4x3 + 9x2 + 4x + 8 given that x = -2 - 2i is a zero of
p(x) . Write your answer as a list. For instance, the solution set is {2, -1, 5,
4}
Solution. By the conjugate root theorem, we know
that x = -2 + 2i is also a zero. Hence, (x - (-2 - 2i))(x - (-2 + 2i))
is a factor of p (x) . Let's simplify the expression as following
(x - (-2 - 2i))(x - (-2 + 2i)) = (x + 2 + 2i)(x + 2 - 2i) = x2 + 2x - 2ix + 2x
+ 4 - 4i + 2ix + 4i - 4i2 = x2 + 4x + 8.
Thus, we can write p(x) = x2 + 4x + 8q(x) . To find q(x)
we divide p(x) by x2 + 4x + 8 to obtain
q(x) = x2 + 1 = (x + i)(x + i) and hence the solution set is {±i,
-2 ± 2i} .
[15 pts] Question 3( HW # 11 - Sec 4.4 prob # 31)
Let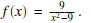 
(a) Determine the domain of f . You may use interval or set notation. For
instance,
Dom(f) = (-∞, -1)∪(-1, 1)∪(1,
∞)or Dom(f) = {x |x ∈ R, x ≠1, -1} .
(b) Determine the x and y intercepts, if any. Label your findings. For instance, the y intercept is y = 4 or located at (0, 4).
(c) Find the vertical, horizontal, or oblique asymptote(s),
if any. Label your findings and be clear. For instance, horizontal
asysmptote is y = 1.
(d) Evaluate the function f at the points x = -8, -4, -2,
2, 4, 8. You may want to write your answer in a tabular form.
( you might find the following information helpful:
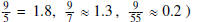
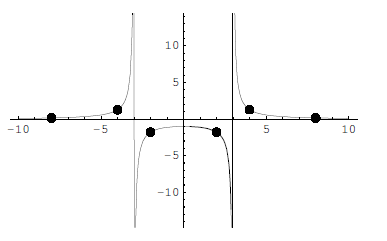
(e) Finally sketch the function f by showing all
asymptotes and intercepts as found in (b) and (c). Also, make sure you
include the points found in (d).
Solution.
(a) Dom(f) = {x |x ∈R, x2 - 9 ≠ 0} = R - {±3}
or Dom(f) = {x |x ∈R, x ≠ 3, - 3}
(b) There is no x intercept since 9 ≠ 0. y intercept: f(0) = -1.
(c) Vertical Asymptote: x = ±3.
Horizontal Asymptote: y = 0 since the degree of numerator is less than the
degree of
denominator , and there is no oblique asymptote, since we cannot have both
horizontal and oblique asymptote at the same
time.
(d) Note that f(x) = f(-x) , and hence
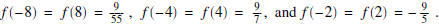
(e) Graph :
[15 pts] Question 4(HW # 12- Sec 4.5 prob # 14)
Find the partial fraction decomposition of
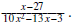Indicate your final answer. For instance,
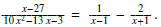
Solution. See HW # 12: Sec 4.5 prob # 14.
[15 pts] Question 5
Solve the following exponential equation for x. Write your
answer as a list. For instance, the solution set is {2, -1, 5} .
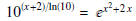
Solution. We solve the problem as following.
Take the natural log of both sides of equation to obtain
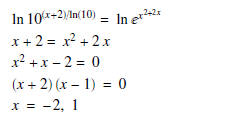
Hence, the solution set is {-2, 1} .
[15 pts] Question 6(HW # 16- Sec 5.5 prob # 30)
Solve the following logarithmic equation for x . Write
your answer as a list. For instance, the solution set is {2, -1, 5} .
ln(x + 1) = ln(3x + 1) - lnx
Solution. See HW # 16: Sec 5.5 prob # 30 .
[15 pts; Extra Credit ] Question 7
Note. Do either of (a) or (b). Do not do both. If you do
both, tell me which one you want me to grade.
You might find the following information helpful:
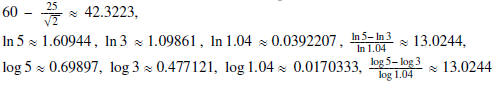
(a) A bottle of baby formula is initially at 10 degree C.
It is placed into a water bath kept at a constant temperature of 60
degrees C. According to Newton's law of cooling , the temperature of the bottle,
T(t) , will follow the rule
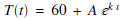where t is measured in minutes. After 10
minutes in the water bath the temperature of the bottle is 35
degrees C. What is the temperature of the bottle after a total of 15 minutes in
the water bath? Express your answer without
exponents or logarithms . Hint. Identify the given information, and write them as
equations and solve for A first, then k .
Once A and k are found, you can easily evaluate T(15) .
(b) A principal of $3000 is invested at 4 % interest,
compounded annually . How many years will it take to accumulate
$5000 or more in the account? Hint. Use the discrete model; identify the given
information into the formula, set up the
inequality and then solve it.
Solution.
(a) We know that T(0) = 10 since we're told that the initial temperature of the
bottle is 10 degrees C. Thus, we obtain
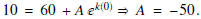Since the temperature of the bottle after 10
minutes is 35 degrees C, then we know that
T(10) = 35. Thus, we obtain the equation
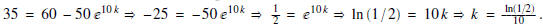
Hence,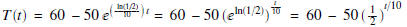 
To find the temperature of the bottle after 15 minutes, we
need to evaluate
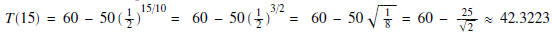
Hence, the temperature of the bottle after 15 minutes is ≈ 42.3223 degree C.
(b) Since the interest is compounded annually, then we use
the discrete model given by the equation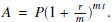 
Now
r = 0.04, m = 1, P = 3000, and we want the time it takes the investment
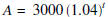to be $ 5000 or more. Hence,
we need to solve the exponential inequality given by
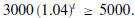We solve it as following
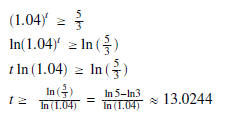
Hence, it takes about 13.0244 years for the principal to grow to $5000 or more.
| Prev | Next |