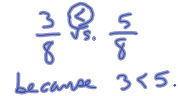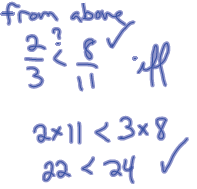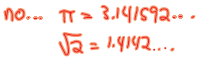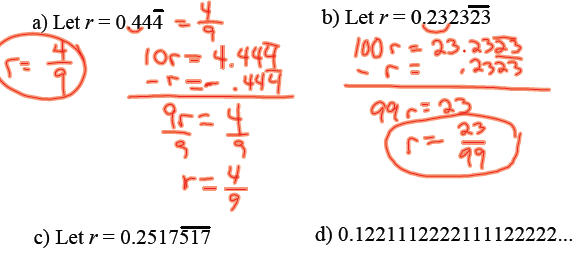Get it on Google Play Get it on Apple Store

Comparing & Connecting Rationals

Agenda:
- Return & discuss the Quiz
- Collect homework; will discuss on Tues.
- Handout exam review sheet
- Discuss Sec. 6.5
- Comparing , Connecting Rationals

Homework: Sec. 6.5
1, 4, 5, 7, 8, 9, 10, 21, 23, 27

Sec. 6.5 - Comparing & Connecting Rationals

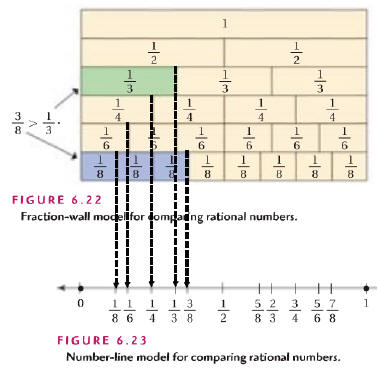
 Area model:
(show 3/8 > 1/3)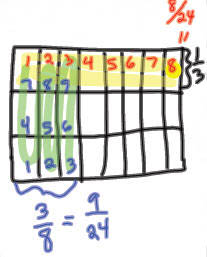

 

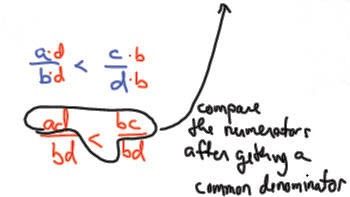
How do we compare fractions with paper & pencil techniques?
If the denominators are the same ...

 

 
Our book says:

a/b < c/d if and only if ad < bc.

Why

 

 

 

The rational numbers have a denseness property (which states
that a rational number can always be found between any two
rational numbers .

The study of rational numbers is the first time students work
with a set of numbers that is dense rather than discrete.

This means we should avoid statements like :
0.6 is the number right next to 0.5, or
3/5 is the fraction between 2/5 and 4/5

 

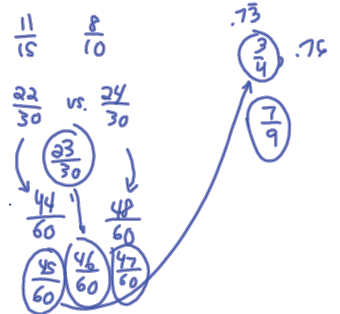
Exercise: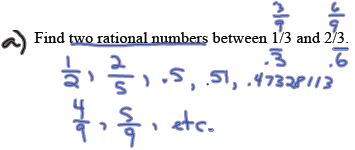



b) Find three rational numbers between 11/15 and 0.8.

 

So we know the set of rational numbers is dense ("there exists a
rational number between any two rational numbers").
Does this imply...

a) That there are an infinitely many rationals between any two
rational numbers? Yes



b) That all points on the number line represent rational numbers?



c) That there is no 11
correspondence between the set of rationals and the set of integers?

 

We have seen that every terminating or repeating decimal is
rational (i.e., it can be expressed as a ratio of two integers .)

Let's see how we can find these fraction representations ...

The easy case terminating decimals :

 

The interesting case repeating decimals :
Prev Next