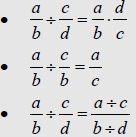The Rational Numbers
Properties of Rational Number Multiplication
Let
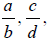and
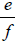be any rational numbers .
• Closure:
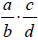is a rational number.
• Commutative:
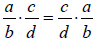
• Associative:
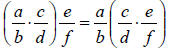
• Identity:
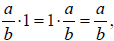where 1 can be represented as m/m, for m ≠ 0
• Multiplicative Inverse :
,
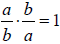where the multiplicative inverse is called the
reciprocal .
o Over Addition :
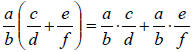
o Over Subtraction :
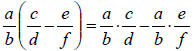
| Division Let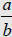 
and
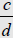be any rational numbers. Then
 |
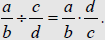There are three methods used to perform rational number
division , as the following
theorem illustrates.
| Theorem Let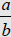 
and
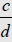be any rational numbers where
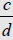is nonzero. Then the following areequivalent .
|
Ordering Rational Numbers
There are four equivalent methods to order rational numbers.
• Number- line Approach :
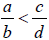if and only if a/b occurs to the left of c/b on the
number line.
• Common -Positive- Denominator Approach : Let b > 0 . Then
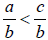if and only if
a < c .
• Addition Approach :
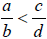if and only if there is a positive rational number p/q
such that
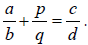Alternatively,
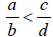if and only if
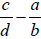is positive.
• Cross-Multiplication Approach: Let b > 0 and d > 0 .
Then
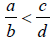if and only if
ad < bc .
Properties of Ordering Rational Numbers
• Transitive: If
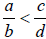and
,
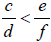then
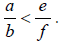
• Addition: If
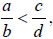then
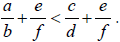
• Multiplication:
o By a positive number
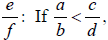then
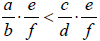
o By a negative number
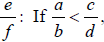then
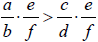
• Density Property: If
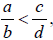then there exists a rational number
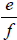such that
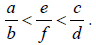
| Prev | Next |