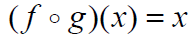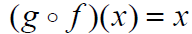Inverse Functions
Recall: The inverse of a function f is a function itself if and only if f is one-to-one.
| Let f be a one-to-one function. Then g is the
inverse function of
f if |
If g is the inverse function of f, then we write g as f-1(x) and read: “f-inverse”.
Example: Determine whether the following functions are inverses of each other:
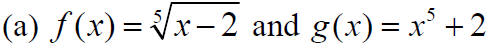
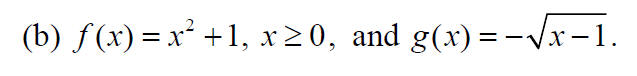
Cancellation Rules for Inverses
| The inverse functions undo each other with
respect to the compositions: f-1( f (x)) =
x for all x in the domain of f |
Equivalent Form of the Cancellation Rules:
| f (x) = y | <-> | f-1( y) = x |
| (x in domain of f) | (y in the domain of f-1) |
Note on the Domains and Ranges of the Inverses:
| Domain of f-1 = Range of f Range of f-1 = Domain of f |
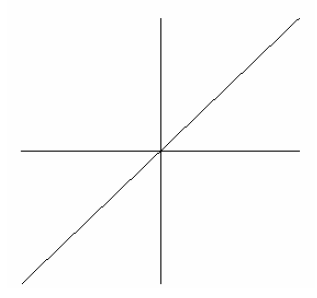
Graphing Inverses :
If the graph of f is the set of points (x, y), then the
graph
of f-1is the set of points ( y, x).
Since, points (x, y) and ( y, x) are symmetric with
respect to the line y = x
then
| the graphs of f and f -1 are symmetric with
respect to the line y = x. |
Example: Given the graph of y = f (x). Draw the graph of its inverse.
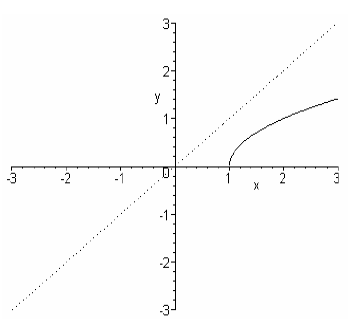
Finding the Inverse of a One-to-one Function f:
1. Write y = f (x).
2. Solve the equation for x : x = f-1 ( y)
3. Interchange x and y.
4. Give your answer in terms of f -1 (x).
Note: Consider all restrictions on the variables.
Example: Find f-1(x), if it is possible.
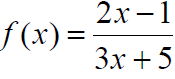
Finding the Inverse of a Domain-restricted Function:
(a) Find the inverse of
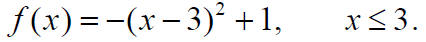
(b) The function
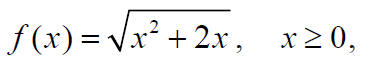
is one-to-one.
Find f-1(x) and its domain and range.
| Prev | Next |