Properties of Exponents
The following properties apply to exponents:
1. 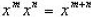 (bases are the same
and we are multiplying the two together , then we
(bases are the same
and we are multiplying the two together , then we
add the exponents ).
2. 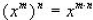 (When we are raising it to a power, we
multiply the exponents).
(When we are raising it to a power, we
multiply the exponents).
3. 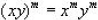 (This is like the distributive property
of exponents, even though that
(This is like the distributive property
of exponents, even though that
name doesn't exist, we still treat it act like. We apply the exponents to
everything inside
of the parenthesis .
4. 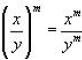 (again similar to property 3, we apply
the exponent to everything).
(again similar to property 3, we apply
the exponent to everything).
5. 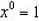 ( anything to the zero power is always
equal to one)
( anything to the zero power is always
equal to one)
6. 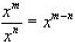 (notice again the bases are the same on
the top and bottom)
(notice again the bases are the same on
the top and bottom)
7. 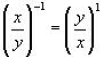 (anytime we have a fraction to a negative
number, we flip the entire
(anytime we have a fraction to a negative
number, we flip the entire
fraction and the negative exponent becomes positive. I actually put a negative
one in this
problem but it could be any negative number).
8. 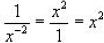 (whenever we have anything to a negative
power, we can take it
(whenever we have anything to a negative
power, we can take it
opposite of where it is….If it is in the denominator, we take it to the
numerator, if it is in
the numerator, we take it to the denominator…..once we take it opposite of where
it is, it
becomes a positive exponent ). This doesn't apply to negative numbers, just
negative
exponents.
9. 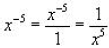 (notice here we didn't have a fraction to
begin with, so our first step
(notice here we didn't have a fraction to
begin with, so our first step
is to write it in fraction form and then take it opposite of where it is. Notice
on property 8
and 9, I have actually plugged in numbers, these can actually be any negative
number!
RADICAL REVIEW
Before we dive in, lets review radicals a little bit. The number in the
little slot
in the front of the radical is called our index.
Example:
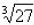 , our index is 3
, our index is 3
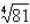 , our index is 4
, our index is 4
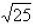 , our index is 2 (note if there is no number,
the index will be 2 by
, our index is 2 (note if there is no number,
the index will be 2 by
default)
Our index tells us how many times a number ( or variable )
should be
multiplied by itself before we can take it out of the radical.
Example:
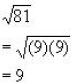
Since our index was 2 and we found that 9 times 9 gives us
81, we brought the
9 out.
Example:
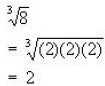
Since our index was 3 and we found 2 times itself three times gives us 8, we
could bring a 2 out.
Sometimes, we have to leave things in the radical:
Example:
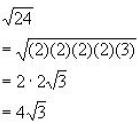
Notice in this example, we didn't have a pair of threes to bring out!
Again, you have seen this material before, the difference is that now we are
going to mix
in radicals before we do these operations . The first thing we need to look at is
how to go
from radical form to exponential form:
RADICAL FORM ->EXPONENTIAL FORM
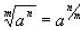
Example:
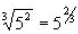
Example:
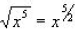
(remember if there is no number for the index , it is 2 by default!)
Example:
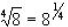
(remember if there is no power on something, it is the invisible 1 by default)
EXPONENTIAL FORM ->RADICAL FORM
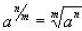
(just like you would expect, in reverse)
BUT WHY?
Radicals are bad enough but fractional exponents, that’s even worse! We do
it so we can
use our properties above.
Example:
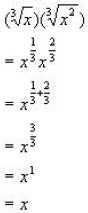
Even though fractions aren't that nice, they are infinitely better than working
with
radicals because we can take advantage of all our properties of exponents.
Simplifying a Number that has a fractional exponential
with a number greater than one
in the numerator
Example:
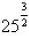
We always split these up. We put the numerator on the
outside of a pair of parenthesis:
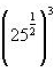
This is going backwards from the property that allows us
to multiply exponents together
when raising it to a power. We then change the inside to a radical form and
simplify it,
then take it to the power on the outside:
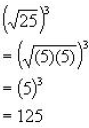
Lets look at one with a negative power:
Example:
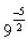
Same step:
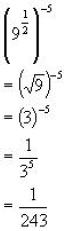
| Prev | Next |