Solving Rational Equations

In section 2–3 we solved equations that had fractions with whole numbers for the denominators. In
that section we solved the equations by first using the multiplication property of equality to multiply
every term in an equation by the Least Common Denominator. When we multiply each term by
the LCD the resulting equation will not have any fractions in it. We can then solve this equation by the
methods of chapter 2.

Example

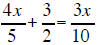	multiply all 3 terms by 10
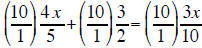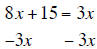	subtract 3x from both sides
5x +15 = 0	subtract 15 from both sides
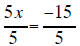	( divide both sides by 5)
x = –3

Solving Rational Equations

All of the Rational Equations in this section will contain terms with denominators that are contain
polynomials instead of whole numbers.

When we solve the rational equations in this section we will use the same method as before. We start
by multiplying every term in an equation by the Least Common Denominator. The difference in
this section is that the LCD will not be a whole number as it was in section 2–3.

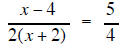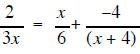The LCD is 4(x + 2)	The LCD is 6x(x + 4)

How to solve a Rational Equation

1. Factor each denominator if possible

2. Find the LCD for all the denominators.

3. Multiply every term in the equation by the LCD. Cancel and reduce . This will leave you with an
equation without fractions .

4. Solve the equation.

5. Check your solution. If the solution makes any of the denominators of the original rational equation
zero then they cannot be used and there is no solution or

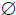
Example 1	Example 2
Solve for x	Solve for x
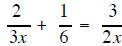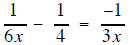the LCD is 6x so mutiply each term of the equation by 6x	the LCD is 12x so mutiply each term of the equation by 12x
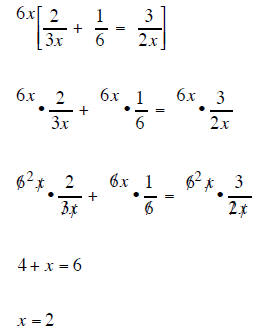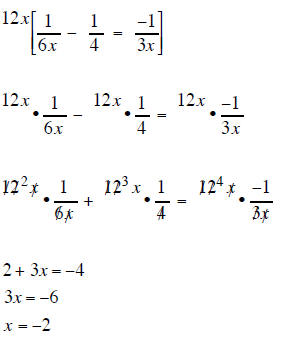(2 does not cause 0 in denominator so)	(−2 does not cause 0 in denominator so)
x = 2	x = −2

Example 3	Example 4
Solve for x	Solve for x
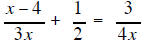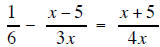the LCD is 12x so mutiply each term of the equation by 6x	the LCD is 12x so mutiply each term of the equation by 12x
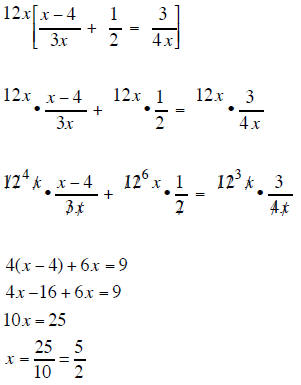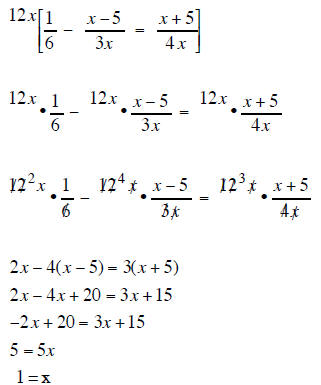5/2does not cause 0 in denominator so	1 does not cause 0 in denominator so
x =5/2	1 = x

Example 5	Example 6
Solve for x	Solve for x
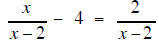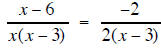the LCD is (x − 2) so mutiply each term of the equation by (x − 2)	the LCD is 2x(x − 3) so mutiply each term of the equation by 2x(x − 3)
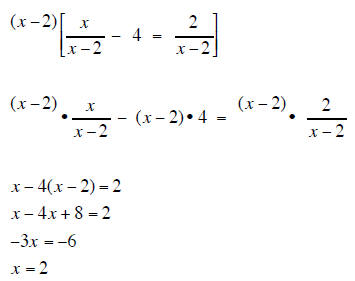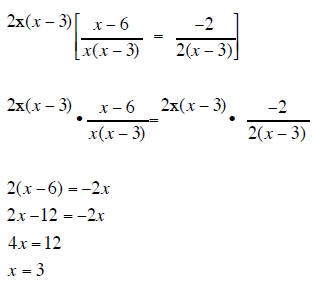2 does cause 0 in denominator so	3 does cause 0 in denominator so
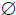or No Solution	or No Solution

Example 7

Solve for x

factor each denominator

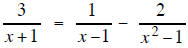
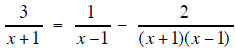
the LCD is (x +1)(x −1) so
mutiply each term of
the equation by (x +1)(x −1)

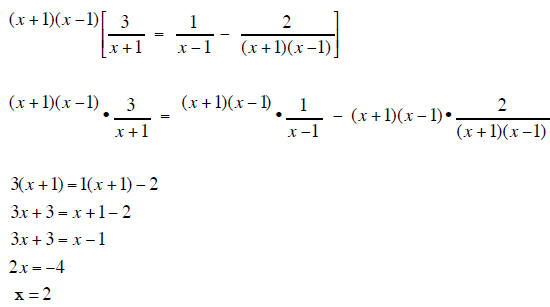
2 does not cause 0 in denominator so
x = 2

Example 8

Solve for x

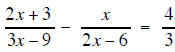
factor each denominator

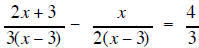
the LCD is 6(x − 3) so
mutiply each term of
the equation by 6(x − 3)

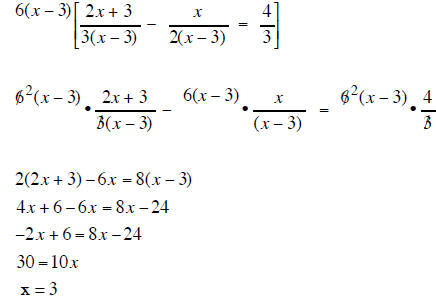
3 does cause 0 in denominator so
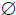or No Solution