Synthetic Division
Synthetic division is a shortcut method to divide a polynomial by a binomial.
Example 1:
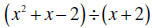
Step 1: Do a countdown on the exponents in the
dividend. The exponents go 2, 1, 0.
The countdown must go from the highest exponent down to 0.
Step 2: Write just the coefficients of the dividend. 1 1 −2
Step 3: Change the sign on the divisor. x +
2 → Use −2.
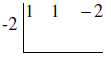
Put the coefficients inside a box and the opposite of the divisor outside the
box.
Bring the first number down outside of the box.
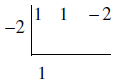
Multiply the number at the bottom by the divisor number (−2) and put the product
inside the box.
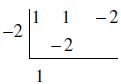
Add the numbers inside the box and bring their total down outside the box.
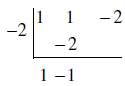
Multiply again.
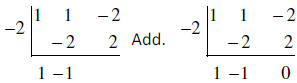
The last number outside the box is the remainder. Here the
remainder is 0. The other
numbers are the coefficients on the polynomial answer . Subtract one from the
highest
exponent (2 – 1 = 1) and that becomes the highest exponent on your answer .
Answer: x – 1
Example 2:
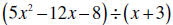
Always do a countdown on the exponents. (2, 1 , 0) Remember to change the sign
on
the divisor .
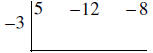Bring the first number down.
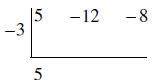Multiply.
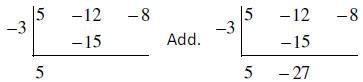Multiply.
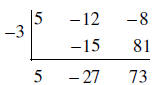
73 is the remainder. Answer: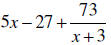
Example 3:
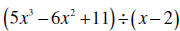
Always do a countdown on the exponents. 3, 2, 0 since the
“1” is missing, we have the
rewrite the dividend as 5x3− 6x2 + 0x +11. Adding 0x does not change the
problem, but
we can now do a countdown 3, 2, 1, 0. Remember to change the sign on the
divisor.
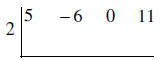Bring the first number down.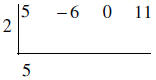
Multiply.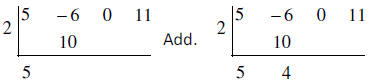
Multiply.
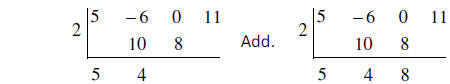Multiply.
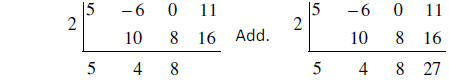
27 is the remainder. Since the highest exponent on the
dividend was 3, subtract 1 and
the highest exponent on the answer will be 2. Answer:
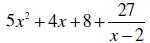
Example 4: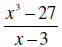
To complete the countdown, we must rewrite the dividend as
x3 + 0x2 + 0x − 27 .
Answer: x2 + 3x + 9
| Prev | Next |