Synthetic Division Review

Review: Synthetic Division
■ Find (x² - 5x - 5x³ + x⁴) ÷ (5 + x).

Factor Theorem
■ Solve 2x³ - 5x² + x + 2 =0 given that 2 is a
zero of f (x) = 2x³ - 5x² + x + 2.

Lesson 2.5, page 312
Zeros of Polynomial
Functions

Introduction

Polynomial	Type of Coefficient
5x3 + 3x2 + (2 + 4i) + i	complex
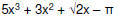	real
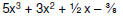	rational
5x3 + 3x2 + 8x – 11	integer

Rational Zero Theorem
If the polynomial

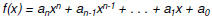
has integer coefficients, then every rational _____
of f(x) is of the form

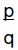
where p is a factor of the ________ coefficient a ₀
and q is a factor of the ________ coefficient a_n.

Rational Root (Zero) Theorem
(in other words)
If “q” is the leading coefficient and “p” is the
constant term of a polynomial , then the only
possible rational roots are ± factors of “p”
divided by ± factors of “q”. (p / q)

Rational Root (Zero) Theorem
(in other words)
Example: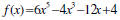
■ To find the POSSIBLE rational roots of f(x), we need the
FACTORS of the leading coefficient (6 for this example)
and the factors of the constant term (4, for this example).
Possible rational roots are

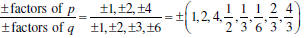
See Example 1, page 313.
■ Check Point 1: List all possible rational zeros
of f(x) = x³ + 2x² – 5x – 6.

Another example
■ Check Point 2: List all possible rational zeros
of f(x) = 4x⁵ + 12x⁴ – x – 3.

How do we know which possibilities
are really zeros (solutions)?
■ Use trial and error and ________ division to
see if one of the possible zeros is actually a
zero.

■ Remember: When dividing by x – c, if the
________ is 0 when using synthetic division,
then c is a zero of the polynomial.

■ If c is a zero, then solve the polynomial
resulting from the synthetic division to find the
other zeros.

See Example 3, page 315.
■ Check Point 3: Find all zeros of
f(x) = x³ + 8x² + 11x – 20.

Finding the Rational Zeros of a Polynomial
1. List all ________ rational zeros of the polynomial
using the Rational Zero Theorem.

2. Use synthetic division on each possible rational zero
and the polynomial until one gives a remainder of
________. This means you have found a zero, as
well as a factor.

3. Write the polynomial as the ________ of this factor
and the quotient.

4. Repeat procedure on the quotient until the quotient is
________

5. Once the quotient is quadratic, factor or use the
quadratic formula to find the remaining real and
imaginary zeros.

Check Point 4, page 316
■ Find all zeros of
f(x) = x³ + x² - 5x – 2.

List all possible zeros, and use synthetic division
to test and find an actual zero. Then use the
quotient to find the remaining zeros.
■ f(x) = x³ – 4x² + 8x - 5

More review -- List all possible zeros. Use synthetic
division to test and find an actual zero. Then use the
resulting quotient to find the remaining zeros. (HW #13)
■ f(x) = x³ + 4x² - 3x - 6

How many zeros, not necessarily rational, does
a polynomial with rational coefficients have?

■ An nth degree polynomial has a total of n ________.
Some may be rational, irrational or complex.

■ Because all coefficients are RATIONAL, irrational roots
exist in ________ (both the irrational # and its conjugate).
________ roots also exist in pairs (both the complex # and
its conjugate).

■ If a + bi is a root, a – bi is a root

■ If 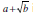is root, 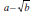is a root.

■ NOTE: Sometimes it is helpful to graph the function and
find the x- intercepts (zeros) to narrow down all the
possible zeros.

See Example 5, page 317.

■ Check Point 5

■ Solve: x⁴ - 6x³ + 22x² - 30x + 13 = 0.

Fundamental Theorem of Algebra
(page 318)

■ If f(x) is a polynomial function of degree n,
where n ≥ 1, then the equation f (x) = 0 has at
least one complex zero, real or imaginary.

■ Note: This theorem just guarantees a zero
exists, but does not tell us how to find it.

Linear Factorization Theorem, pg. 319

Remember…

■ Complex zeros come in pairs as
complex conjugates: a + bi, a – bi

■ Irrational zeros come in pairs.

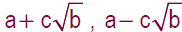
More Practice

Find a polynomial function, in factored
form, of degree 5 with -1/2 as a zero
with multiplicity 2, 0 as a zero of
multiplicity 1, and 1 as a zero of
multiplicity 2.

Practice
Find a polynomial function of degree 3
with 2 and i as zeros.

See Example 6, page 319.

■ Check Point 6, page 320

■ Find a third-degree polynomial function f(x)
with real coefficients that has -3 and i as
zeros and such that f(1) = 8.

Solve the given polynomial equation. Use the
Rational Zero Theorem, or graph as an aid to
obtaining the first zero.

■ x⁴ – x³ + 2x² – 4x – 8 = 0.

Extra Example
Suppose that a polynomial function of degree 4
with rational coefficients has i and
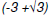
as zeros. Find the other zero(s).

Extra Example
Find a polynomial of degree 3 where 4 and 2i
are zeros, and f(-1) = -50.

■ Use the Rational Zero Theorem to list all the
possible zeros for
f(x) = 4x⁵ – 8x⁴ – x + 2.