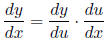The Chain Rule
Suppose we have two functions , y = f(u) and u = g(x), and we know that y
changes at a rate
3 times as fast as u, and that u changes at a rate 2 times as fast as x (ie.
f'(u) = dy/du = 3 and
g'(x) = du/dx = 2). What if anything can we say about
,
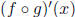the derivative of the composition
?
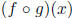It stands to reason that y should change at a rate 6 times as fast as x, so we
would
find
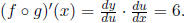The chain rule asserts that our intuition is correct, and provides us
with a means of calculating the derivative of a composition of functions, using
the derivatives of
the functions in the composition.
| The Chain Rule Suppose f(u) is differentiable at u = g(x), and g(x) is differentiable at x. It follows that the composite function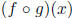
is differentiable at x, and that
If y = f(u) and u = g(x), then
where dy/du is evaluated at u = g(x). |
Many undergraduate calculus texts assert the following proof of the chain rule.
Purported Proof of the Chain Rule:
Recall that
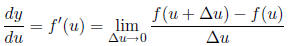
and let
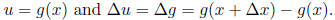It
follows that
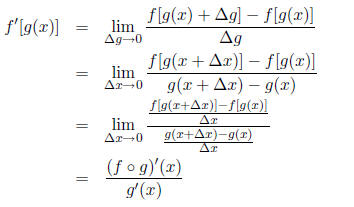
We are able to replace
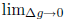with
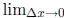as
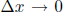implies
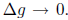If we multiply both
sides of the equation with g '(x), then the proof follows.
This proof feels very intuitive, and does arrive to the conclusion of the
chain rule. However, there
are two fatal flaws with this proof. The first is that although
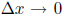implies
,
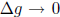it is not
an equivalent statement . It is very possible for
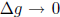while x does not approach 0. This
leads us to the second flaw with the proof. Let g(x) be a constant function. It
follows that for
every x and
.
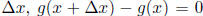This means that the above derivation included division
by 0, which is clearly not permitted by the rules of mathematics . For those
reasons we will have
to discard the above proof, but we currently do not possess the tools to
properly prove the chain rule.
In the composition f(g(x)) we refer to f as the outer function, and g as the
inner function. We can
describe the basic mechanism of the chain rule as follows: differentiate the
outer function holding
the inner function as a constant. Then, multiply the result by the derivative of
the inner function.
If there is a composition of more than two functions, the above process is
simply repeated as many
times as necessary. Consider the following examples.
Example 1 Find the derivative of
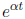(with respect to t),
.
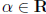Solution The above function is a composition of two functions, et and t. Thus, we
can apply the
chain rule. We take the derivative of the outer function (which is et), evaluate
the result at the
inner function (αt), differentiate the inner function (yielding α), and then
multiply the results.
Thus, to find the derivative of an exponential function
where the argument is multiplied by a
constant, simply multiply the exponential function by that constant. This is
consistent with the
derivative of the exponential function, where that constant is simply a 1.
Example 2 Find the derivative of
.
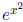Solution Once again we can apply the chain rule, to the composition of
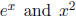. We take
the derivative of the outer function (which is
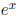), evaluate the result at the inner function
(x2),
differentiate the inner function (yielding 2x), and then multiply the results.
Example 3 Find the derivative of
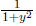(with respect to y).
Solution In order to solve this problem it is helpful to first rewrite the
function as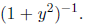 
Then we can see there is a composition of two functions
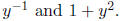Applying the chain rule
we find
Example 4 Find the derivative of
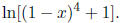
Solution In this case we have a composition of three functions
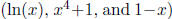. Fortunately
it is simple to repeatedly apply the chain rule, and doing so we find that we
only need to multiply
by the derivative of each composed function to find the derivative of the entire
composition.
Example 5 Find the derivative of 2t
(with respect to t) using the chain rule.
Solution We previously calculated this derivative using the definition of the
limit, but we can
more easily calculate it using the chain rule. Write 2 =
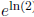, which can be done as the exponential
function and natural logarithm are inverses . Now take the derivative using the
chain rule
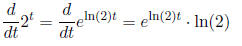
| Prev | Next |