Semidefinite Programming

Two remarks on previous lecture

• Fact 9 shows that pd (or psd) can be verified by checking that every principal minor
is positive (or nonnegative). For pd we only need to examine leading principal minors.
However, this does not work for verifying psd as

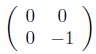
shows. This matrix has leading minors equal to zero but a negative trailing minor.

• Fact 10 has introduced the Schur complement. If

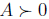
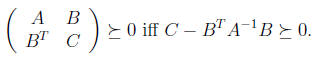
This lends itself to showing that the Cholesky factorization of a pd matrix exists.

Fact 11 (Representing quadratics) Given 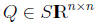the quadratic form

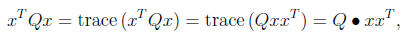
while a quadratic function of x, is a linear function of X := xx^T .

Fact 12 If U and V are psd, then U • V≥0 (used in showing weak duality for SDPs). In
fact, we have the following theorem.

Theorem 1 If 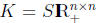, then K is self-dual,

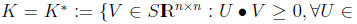
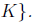
Proof: Part 1: showing 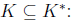want to show that if
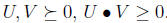
Demonstration 1: By facts 3, 4, and 6 we can assume that one of U, V is diagonal. But then
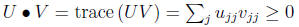(need only look at the diagonal entries).
Demonstration 2: By Fact 1, and the existence of matrix square roots ,

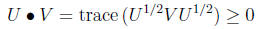
since 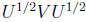is psd (Fact 7) and so its trace is nonnegative

Part 2: showing 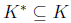by contraposition, i.e., if
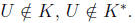
If 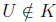, then by definition there exists a z such that 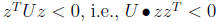(by Fact 11).
But 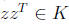by Corollary 1, so

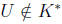
By the same argument, if 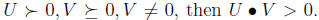This shows a similarity
between nonnegative vectors and the cone of psd matrices.

Fact 13 If 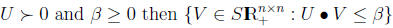is compact.
Proof: The set is clearly closed, so need to show it is also bounded. Suppose
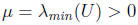
(since 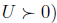Then

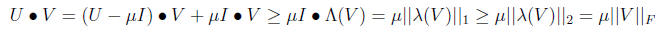
for any 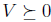So any V in the set has

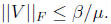
Fact 14 If
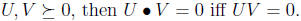
Proof: First note that if UV = 0 then clearly U • V = trace (UV ) = 0. To show the
converse suppose 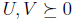with U • V = 0. Then

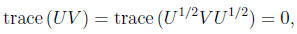
so 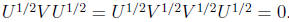Define 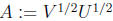to obtain the condition A^TA = 0.
This implies A = 0 since the diagonal entries of A^TA are the squares of the 2-norms of the
columns of A. But 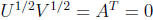easily gives UV = 0.

Fact 15 If 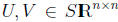then U, V commute iff UV is symmetric, and iff they can be
simultaneously diagonalized , i.e., iff we can find Q, 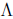,M (Q orthogonal, 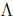,M diagonal) with

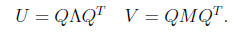
Proof: Omitted, since part of HW1.

Applications

Matrix and NLP optimization problems

We have already shown how to minimize the maximum eigenvalue of a symmetric
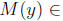
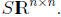
What if M(y) is not symmetric and not necessarily square ? For example, say we want
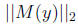as small as possible. Recall:

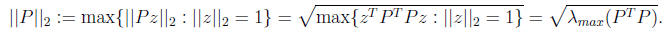
Lemma 1

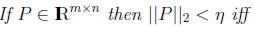
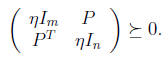
Proof: Observe that the above matrix retains linearity w.r.t. η, y. Examine two cases:
If P = 0, then both conditions reduce to
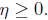
If P ≠ 0,

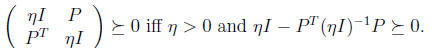
With η > 0, the last condition is equivalent to 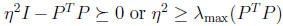which holds
iff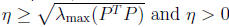which is what we needed to show.
Note that we have also shown that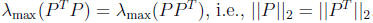

So, 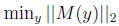is equivalent to

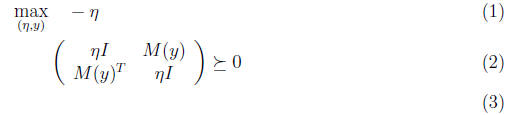
which is the desired SDP in dual form.

Linear programming and nonlinear programming

Consider first an LP in dual form

and try to rewrite it as an SDP. The constraint

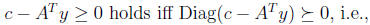
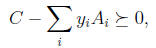
where C = Diag(c) and Ai_i = Diag(a_i) and a_i is the ith column of A^T . This gives the equivalent
SDP in dual form.

Now consider a correspondence between primal LP and SDP. The primal SDP is given by

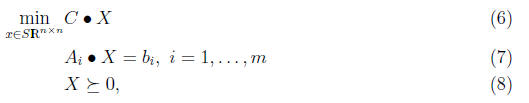
whereas the primal LP is given by

In general, our SDPs may have block diagonal form. Suppose 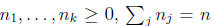and
define

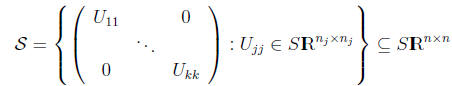
If C and all A_i’s are in S then automatically 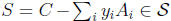for any The primal
problem involves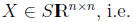

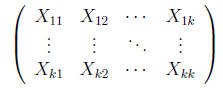
but we can restrict X to S without loss of generality (see HW1). Applying this to the primalform
SDP above we can assume that X is diagonal, so that it reduces to the primal -form
LP.