The Fundamentals: Algorithms, Integers, and Matrices

Section 3.6 Integers and Algorithms

Representation of integers in bases other than 10

• Theorem 1: (Representing a number in any base b, where b is a positive
integer greater than 1). Any number n can be written uniquely in the form

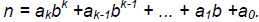
where k is nonnegative integer, and 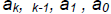are nonnegative
integers less than b.
Examples: b = 10

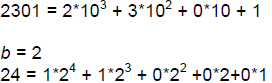
Thus the binary (base 2) representation for 24 is
(1 1 0 0 0)₂

• Hexadecimal Expansion: Base 16.
Digits 0-9 and A, B, C, D, E (for 10 through 15)
• Examples 3, 4, 5 show algorithm to convert base 10 to other bases (such
as 8)

Algorithm constructing expansion (page 221):
o Divide the number by base -- remainder will be rightmost digit.
o Divide the resulting quotient by base -- remainder will be the next
rightmost digit.
o Keep doing this until q quotient of 0 is obtained.
Pseudocode page 221 bottom

Example 6: Converting between hexadecimal, octal, and binary.
From binary to hexadecimal:

Group into blocks of four (from right -- adding 0's to left if
necessary).
Convert each block of four binary digits into corresponding
hexadecimal number (see Table 1, page 222)

Skip sections for Algorithms for Integer Operations and Modular
Exponentiation

The Euclidean Algorithm
• An algorithm for finding the gcd of two numbers . Oldest known algorithm
(Euclid -- 325-265 BCE)
• Method :
o To find the greatest common divisor of two numbers a nd b, where
a > b. (Say a = 287, b = 91):
o Write a = bq + r.
o If r is 0, then gcd = b (why?)
o Otherwise gcd (a,b) will be gcd(b,r) (Proven in Lemma 1 -- we
won't cover the proof)
o So repeat the above process to compute gcd(b,r).
o Keep doing this until a remainder of 0 is obtained.
o The gcd will then be the final value of b .
• Example 12 page 229 gcd(414, 662) = 2.

Section 3.8 Matrices

This section provides a foundation for work in future chapters.
• Matrix: Rectangular array of numbers
• Dimension of matrix is m x n, where m is the number of rows and n is
the number of columns in the matrix.
• Example 1 gives a 3 x 2 matrix.
• Matrices are normally represented with capital letters (A, B, C).
• Individual elements or entries of arrays are referenced by their row and
column index.
• a_ij is the element in the ith row and jth column.

Matrix Arithmetic

• Matrix Addition: If matrices A and B are both m x n matrices, then the m
x n matrix A + B is the matrix obtained by adding the elements in the
corresponding rows and columns of A and B.
• Matrix Multiplication: The product AB, of two matrices A and B, is
defined when A is m x k and B is k x n. In this case the product is an m x n
matrix obtained by calculating the ij'th element, c_ij, of AB as
c_ij = the sum of the products of the corresponding
elements from the ith row of A and the jth column of
B.
• Example 3 shows the computation of the product of 4 x 3 matrix A and 3 x
2 matrix B. Note that the product BA does not exist.
• Example 4 shows matrix multiplication is not commutative. (AB is not in
general equal to BA)
• Algorithm 1, page 249 gives a pseudocode representation for a
straightforward matrix multiplication algorithm .
o The number of additions and multiplication's required for this
algorithm can be calculated as follows : To calculate one entry in the
product matrix, we must perform k multiplications and k-1 additions.
There are m*n entries in the matrix.
o Thus the total number of multiplications is m*k*n and the total
number of additions is m*n*(k-1).
o If A and B are both n x n matrices, the total number of
multiplications is n³ and the total number of additions is n³-n²
o Thus as a function of n, the total number of additions and
multiplications for AXB is 2n³-n², which is O(n³). We therefore say
that this has time complexity O(n³).
• Matrix multiplication is associative -- that is .
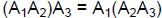• Which order requires the least number of multiplications?

• Example 6: Assuming dimensions are A₁ is 30 x 20, A₂ is 20 x 40, and A₃
is 40 x 10.
o Resulting matrix is 30 x 10.
o (A₁A₂)A₃: 36000 total since:
To calculate A₁A₂ , a 30 x 40 matrix, requires 30*20*40 =
24000 multiplications.
To calculate the product of A₁A₂ and A₃ requires 30*40*10 =
12000 multiplications.
o A₁ (A₂A₃): 14000 total since:
To calculate A₂A₃ , a 20 x 10 matrix, requires 20*40*10 =
8000 multiplications.
To calculate the product of A₁ and A₂A₃ requires 30*20*10 =
6000 multiplications.

Transposes and Powers of Matrices

• The n x n Identity Matrix I_n: i,j'th element is 1 if i = j, 0 otherwise.
• If A is an m x n matrix, then A I_n = I_m A = A.
• A square matrix is an n x n matrix.
• Powers of square matrices: A⁰ = I_n. Aⁿ = A A A …. A (n-times).
• A^t denotes the transpose of a matrix A: A^t is obtained from A by
interchanging the rows and columns. That is the i,jth element of A^t is the
j,ith element of A.
• See Example 7.
• A square matrix A is symmetric if A = A^t.

Zero-One Matrices: Matrices whose entries are either 0 or 1.
• Boolean operations:
o join of a zero -one matrix is the 'OR'ing of corresponding elements
o meet of a zero-one matrix is the 'AND'ing of the corresponding
elements.
o Boolean product of two matrices A and B is like multiplication
except we compute the "OR" (instead of +) of the "AND" (instead of
product) of corresponding elements in the ith row of A and j'th
column of B
• See Examples 9 and 10, page 252-253